14 мая 2015 года в рамках проекта «Публичные лекции "Полит.ру"» лекцию на тему «Теория игр в изучении общества» прочитал кандидат экономических наук, доцент факультета экономических наук НИУ-ВШЭ, экономист и политолог Алексей Владимирович Захаров.

Теория игр – прикладная область математики, которая находит применение при анализе взаимодействий между людьми, организациями или государствами, моделируя задачи, где развитие ситуации зависит от нескольких субъектов, принимающих решение, и помогая принять оптимальное решение с учетом информации о других участниках. Она рассматривает ситуации, где есть субъекты (игроки), которые могут действовать так или иначе, у игроков есть определенное число вариантов действий, а также определена функция, которая определяет итог (выигрыш) для игрока в зависимости от выбранного им варианта поведения.

Алексей Захаров рассказал о некоторых хрестоматийных задачках теории игр, например, о «дилемме заключенного». В классическом варианте этой ситуации есть двое заключенных обвиняемых в преступлении. Они содержатся в разных камерах и не могут общаться друг с другом. Полиция предлагает каждому сделку. Если заключенный сознается, а его подельник хранит молчание, то сознавшегося отпускают, а непризнавшегося осуждают на 10 лет заключения. Если сознаются оба заключенных, то обоих приговаривают к восьми годам. А если оба молчат, то получают лишь год тюрьмы.

Оказывается, что если оба заключенных попытаются рассуждать рационально, то в результате они получат не оптимальное для них обоих решение. Первый заключенный будет думать: «Если мой коллега молчит, то лучше сознаться и получить свободу. Если коллега сознался, то мне тоже лучше сознаться, так как 8 лет тюрьмы все-таки меньше десяти». Аналогично думает его коллега. В результате оба сознаются и оказываются в тюрьме на восемь лет, тогда как, если бы оба молчали, то получили бы всего по году.

В реальной жизни можно найти множество ситуаций, в которых условия «игры» соответствуют дилемме заключенного. Развитие гонки вооружений между странами, исчерпание общих ресурсов (например, при рыбной ловле в океане или при выпасе скота на общественном пастбище), применение допинга в спорте – все эти процессы вызваны тем, что каждый из игроков действует в собственных интересах, но это в результате идет во вред интересам всех. Ценовой сговор между двумя компаниями – тоже вариант дилеммы заключенного. Всегда наступает момент, когда выгодно обмануть своего партнера по сговору. Еще один пример, рост затрат на рекламу в двух конкурирующих компаниях. Каждой из них было бы выгоднее сократить эти затраты, но они не делают этого, так как считают, что другая компания не поддержит этой инициативы и получит преимущество.

Еще одна ситуация, рассмотренная Алексеем Захаровым, сводится к следующей игре. На улице к прохожему подходит грабитель и говорит: «Отдавай кошелек, а не то я взорву гранату». Здесь есть два выбора. Прохожий выбирает расставаться ли ему с кошельком, а затем, в случае отказа прохожего, грабитель выбирает взрывать или не взрывать гранату (ведь от взрыва пострадают оба). Здесь выбор прохожего определяется тем, насколько серьезно он оценивает намерения грабителя. Если вероятность, что грабитель взорвет гранату, кажется невысокой, прохожий предпочтет не отдавать кошелек. Данный пример показывает важность «социального капитала» при игре, ведь успех игрока будет зависеть от того, насколько партнеры доверяют его обещаниям. Поэтому важно умение держать эти обещания, даже когда в некоторых случаях приходится действовать в ущерб себе. Этим в частности подтверждается необходимость независимости центрального банка в стране. Если центробанк будет действовать по указу правительства, выпуская дополнительные деньги в случае необходимости, то доверия к валюте этой страны не будет. Никто не станет держать в этой валюте свои сбережения, так как слишком велик риск инфляции.

Интересный пример применения теории игр произошел в 2000 году в американском реалити-шоу Survivor (его аналог на российском телевидении назывался «Последний герой»). Участники должны были на каждом этапе проходить какое-либо испытание, выявляя лучшего в нем. Затем в конце дня они определяли, кто покинет группу претендентов на победу. Иммунитетом в данном случае обладал победитель проходившего в этот день испытания. На последних этапах при определении, кого выгнать, голос победителя оказывался решающим. На стадии, когда оставалось девять участников, выбывшие стали образовывать жюри, которое в самом конце должно было определить из двух финалистов победителя путем голосования. Перед последним испытанием оставалось три претендента. Это были молодые мужчина и женщина: Рич и Келли, а также Руди, которому было уже 72 года. Руди по физическим кондициям сильно уступал конкурентам, но был очень популярен среди участников шоу. В испытании им предстояло стоять на столбе на одной ноге. Через некоторое время после начала Рич сознательно спрыгнул со столба.

Пока Рич стоял на столбе на одной ноге, он решил представить возможные результаты. В случае своей победы ему предстояло бы определить, кого выгонять перед финалом Келли или Руди. Если бы он выгнал Келли, то остался бы в финале с Руди и проиграл, так как участники любят Руди и проголосовали бы за него. Если бы он выгнал Руди, то все равно проиграл бы в финале, так как голосующие не простили бы ему изгнания Руди. Значит победа в последнем испытании с высокой вероятностью означает поражение в финальном голосовании. Если же Рич проигрывает в стоянии на столбе, то победительницей, скорее всего, станет Келли. Она побоится остаться в финале с Руди, поэтому она оставит себе в качестве пары Рича, но навлечет на себя гнев голосующих. Поняв все это, Рич решил спрыгнуть. Его прогноз полностью оправдался: победила Келли, она выгнала Руди, а победа в финальном голосовании досталась Ричу. Интересно, что Рич до этого не получал специальной подготовке в области теории игр, но его рассуждения оказались прекрасным примером анализа игры.

"Пока гремят пушки – музы молчат", – хорошо, что это утверждение не имеет абсолютной силы. Украинские ученые продолжают заниматься исследованиями и думать о том, как привлечь в науку молодых. Об этом читайте в интервью с Сергеем Колядой, докт. физ.-мат. наук, ведущим научным сотрудником отдела теории динамических систем Института математики НАН Украины, президентом Киевского математического общества (2006-2014). Беседовала Наталия Демина.  

• Часть 1. "Украинской Академии нужно радикальное обновление"

Как вы сами решили стать математиком? У Вас были колебания пойти в другую науку?

Я родом из очень маленького села, которое так и называется – Коляды (Полтавская область). Это всего 8 км от того места, где родился Николай Васильевич Гоголь. Мой отец после выхода на пенсию даже работал садовником в музее Н.В. Гоголя. Как я попал в математику? Я ее, конечно, любил. Стандартный путь всех мальчишек из нашего села, которые хорошо учились, был такой: после 8-го класса все шли в один из двух техникумов. Обязательно после 8-го, потому что после 10-го из села могли и не отпустить, могли не выдать паспорт. В два техникума – геолого-разведывательный или строительный. Если после 10-го, то девушки шли в пединститут, других вариантов не было.

И мне повезло, что, после окончания начальной школы, к нам в школу прислали молодую учительницу математики — Мышасту Галину Петровну. Фактически благодаря тому, что она проводила со мной занятия по отдельной программе, я в 7 классе выиграл районную олимпиаду по математике. В это же время в школу прислали телеграмму, что есть такая Киевская физико-математическая школа-интернат при Киевском государственном университете, вроде Колмогоровского при МГУ, Санкт-Петербургского или Новосибирского школ-интернатов.

Завуч мне сказал, что туда поступить невозможно. Меня это немного задело. А еще сказали, что будет два этапа поступления, когда проходят олимпиады: в марте, на каникулах, и потом летом. Нам сказали, что отбор будет проходить сначала в Полтаве. Папа мне дал около 10 рублей на дорогу. Республиканских олимпиад в 7-ом классе тогда еще не было, даже и областных, и я поехал со своей учительницей Галиной Петровной, которая везла 10-ти классника на областную олимпиаду. Потом ей сказали, что надо в Киев ехать. Она мне дала, как сейчас помню, еще 20 рублей (на неделю) и нас (группу школьников из Полтавской области) повезли в Киев.

Отбор я прошел. Было интересно: сдавали письменно и устно математику и физику. Математику на то время я хорошо знал, а физику – никак. Физику у нас вел бывший тракторист, который заочно окончил Полтавский пединститут, и я ее совершенно не знал. Летом на втором этапе поступления было 4 экзамена – математика была письменно и устно, а после нее такая же физика – письменно и устно. Когда я пришел на физику (устно), меня спросил Виктор Тоевич Топоров: «Молодой человек, а вы знаете, какой у нас проходной балл?» Я не знал. Он говорит: «12!» То есть надо было все сдать на «3». «И самое смешное, что вы их набрали!»

Почему он это сказал – потому что, на самом деле, на устном экзамене говорили оценку по письменному. И, поскольку я и еще несколько человек первый экзамен по математике написали на «5», по устному я тоже получил – «5», значит, по физике у меня было «2». Я ему всё рассказал о нашем «трактористе» и др. Я так разнервничался, что даже было сдал черновик, а не ту тетрадь, где решил … одну задачу. Он посмотрел и сказал: «Хорошо, я тебя даже спрашивать не буду. «3» – письменно, «4» – устно». Вот так я поступил. 

Вы были хорошим олимпиадником?

Да, но беда в том, что я поздно «стартовал». Участвовал в республиканских, а на всесоюзные не попадал. В 10-ом классе у нас была сильная не только в рамках Киева, но и всей Украины, олимпиадная компания, там даже «международники» были: Саша Резников, Саша Блох, Миша Любич, Костя Рыбасов, Боря Цыган… В общем, много сильных. Получилось так, что из школы у нас был «свой олимпиадчик». Сам он родом из Севастополя, с малых лет был хорошо подготовлен, два года – в 8-м и 9-м он брал первые места на всесоюзных олимпиадах.

А в 1975 году, когда мы заканчивали школу, были отменены все предыдущие привилегии. Это означало, что нужно было победить на республиканской олимпиаде, победа в предыдущей всесоюзной олимпиаде не учитывалась. Так, скажем, Саша Блох не попал на всесоюзную. Из Украины ехала также отдельная команда из интерната. У нас всегда ехала отдельная команда либо предыдущих победителей, но ездили и сильные ребята по отдельности. И получалось следующее: мой друг (из моего класса) обошел нашего лидера на «республике».

А у меня по двум задачам стояло по «единице», но я же знал, что я их решил! Я пошел на апелляцию. Одним из апеллирующих был известный олимпиадчик в прошлом и математик А.К. Толпыго. Он услышал мои объяснения и поставил мне «5». А следующим я пошел к своему завучу, из нашей школы-интерната. Он был членом республиканского жюри, и он мне не добавил ни одного балла. Я очень обозлился, ничего не понимая. А причина была простая: у нас была небольшая разница с лидером нашей команды. Если бы еще и я обошел его, то были бы проблемы с выбором, кто должен ехать на всесоюзную. Разумеется завуч поступил мудро… и к слову лидер выступил хорошо на олимпиаде, был потом кандидатом на международную…

Но, с другой стороны, я благодарен судьбе, что, может быть, это и к лучшему. Такие моменты в жизни всегда заставляют просто больше работать. Например, своему научному руководителю академику А.Н. Шарковскому я очень благодарен, прежде всего, его не очень хорошим отношением ко мне. Как ни странно может это казаться! Я всегда видел, что могу больше сделать и, когда я что-то делал и получал хорошие результаты, и не очень хорошую оценку этого, меня это заставляло еще больше работать.

Подстегивало?

Да.

Как Вы сейчас оцениваете состояние дел в популяризации математики в Украине, в Киеве? Проводятся ли научно-популярные лекции для простых людей, где рассказывается, что делают современные математики, для школьников?

В Институте Макса Планка по инициативе Хирцебруха была заведена такая традиция: в институте проводился День математики, когда двери открывались для свободного посещений жителей Бонна и окрестностей. В этот день ведущие математики читают лекции так, чтобы их могли понять простые люди, обладающие лишь школьными знаниями математики. Чтобы могли понять, о чем идет речь. Это очень интересно. Здесь я никогда ничего такого не видел. А в 2014 году молодые люди, Сергей Максименко в первую очередь, организовали такое в Институте математики на «Днях науки».

Я был очень поражен! Было четыре лекции на очень популярные темы в математике – Анатолий Самойленко прочитал лекцию «Задача на миллион: гипотеза Римана» (для студентов), Юрий Дрозд – лекцию «Древнегреческая задача о трисекции угла» (для школьников, начиная с 8-классников), Сергей Максименко – «Эйлерова характеристика топологии причесок» (школьники старших классов, студенты), Александр Рыбак – «Математика жонглирования» (школьники старших классов, студенты, действительно будет показываться жонглирование). И это было очень красиво объяснено для всех людей. В математике много таких задач, которые еще не решены, но объяснить проблему можно даже школьнику в начальной школе. И это очень важно! Потому что часто думают, что математики считают что-то такое совсем абстрактное…

Оторваны от жизни.

Да. Я помню, когда в 2001 году мы проводили конференцию-школу в Кацивели, я говорил, что было восемь источников поддержки, и один из них был из CNRS. Надо было написать, на что конкретно нужны деньги, например: «Проезд из Москвы, проживание» и т.д. И вот я уже уехал, во Францию, кажется, а мне супруга пишет: «Я получила за тебя деньги в посольстве Франции. Самое интересно и смешное было тогда, когда я пошла их получать. Женщины, которые мне их выдавали, спросили: «А не могли бы вы нам сказать, что же он такое французам посчитал, что ему такие деньги дают?» Так что для основной массы людей математики: «Что-то там считают», а с другой стороны слышишь: «А что же они такое там считают, там уже нечего делать! Всё уже доказано и посчитано».

Приведу еще один пример популяризации математики. Яков Синай говорил, что у него есть задачка для первоклассников, которых учат складывать числа до 100. «Вот возьмите два двузначных числа (не оканчивающихся на 0), сумма которых равна 100. Скажем 18 и 82. А теперь поменяйте местами цифры. Сколько будет? 109. Взяли других два числа , снова – 109. А теперь докажите, что это будет всегда». Объяснение совсем простое, естественно. Даже ученик 1-го класса может это объяснить. Но надо подумать немного. Это уже анализ проблемы.

В школе не учат думать над какой-то математической проблемой. Учат только решать (олимпиадные) задачи, а это совершенно разные виды деятельности. Надо четко различать олимпиадную математику (иногда шутят «спортивную математику») и просто математику как науку.

Еще к тому, как я математиком стал. Был у нас в классе преподаватель геометрии Леонид Миронович Савченко. Он мне поставил первую «неолимпиадную» задачу. Я над ней думал много дней, даже чуть не написал статью (на первом курсе мех-мата Киевского университета). В принципе, она такая интересная, простая в каком-то смысле. Возьмем треугольник. Известно, что если один угол в два раза больше другого, то между сторонами можно написать соотношение в виде формулы. Теперь пусть один угол в n>2 раз больше другого. Леонид Миронович спросил: «Как написать соотношение и можно ли написать соотношение между сторонами в этом случае или нет?» И я придумывал как это сделать, придумал свои «синусы-косинусы». Потом будучи уже студентом понял, что это связано с многочленами Чебышева. В общем, там уже занятие принимало совершенно другие формы. Я думал над этим постоянно. Такие задачки для школьников очень важны.

Кто из математиков оказал на вас наибольшее влияние?

Самое большое впечатление как личности в математике на меня произвели Яков Синай и Михаил Громов. Прежде всего глубиной понимания … моих результатов, о которых я им рассказывал! Они знают математику в целом, я бы сказал, чувствуют, какие результаты классные, какие – нет.

В первый раз в Москве я был в 1984 году, заехал к Синаю. Ехал по другим делам, но узнал про его семинар. Мне просто хотелось с ним познакомиться. У них был такой замечательный семинар в Институте космических исследований с Георгием Заславским.

С Михаилом Громовым я познакомился в IHES, когда был там в 1997 году. Я рассказывал ему о своих результатах тоже. Но что еще меня поразило. Я его спросил после своего рассказа, вопрос был по топологической динамике. Ответ был сногсшибательным: «Сережа, извините, я очень плохо знаю общую топологию». Он мог бы сказать, что подумает или еще что-то, а он честно сказал, что не знает!

Кстати, оба эти выдающиеся математика получили самую престижную награду в математике – Абелевскую премию!

Математика продолжает Вас волновать? Вы круглые сутки думаете над задачками? Бывает такое, что решаете, не спите?

Как определить математик вы или нет? Преподаватель математики Сергей Рукшин, который был школьным наставником у Григория Перельмана, Стаса Смирнова и многих других математиков сказал такую замечательную на мой взгляд фразу – «Профессионального математика задачи преследуют сутками, месяцами и годами». Значит, если преследуют, то вы – математик. А так ... . Если ты заболел математикой, в хорошем смысле, то вылечить можно только бездельем, если совсем перестанешь думать. 

Конечно, есть задачки, которых сейчас всё больше и больше, на все просто не хватает времени. Но мне, слава Богу, повезло, в последние лет пять у меня появились несколько молодых соавторов. Они были моими учениками, я преподавал им в Киевском национальном университете. И я с ними почти со всеми написал научные работы. Сейчас как раз вышла статья в соавторстве с Юлией Семикиной в «Proceedings of the American Mathematical Society». Она училась тогда на третьем курсе Киевского национального университета. А сейчас учится в аспирантуре в Бонне, скорее всего, она не будет писать у меня Ph.D. 

Но я счастлив тем, что у меня есть сильные ученики и что я написал несколько работ с ними. Просто давал им задачки, даже особо не ожидая, что они их будут решать. Их это тоже захватило, мы вместе с ними сделали статьи. 

У меня есть четыре задачи, которые я приготовил своему аспиранту (показывает на доску). Скажем, он очень знаменитый человек в олимпиадном движении, Саша Рибак. Он победил на трех международных студенческих олимпиадах, из них два раза был абсолютно первым (2004 и 2006). В математических олимпиадах он – если не сильнейший, то очень сильный человек. Одна из проблем с ним у меня такая – он до сих пор «не может заставить себя» долго думать над какой-то задачей. 

«Полит.ру» публикует видеофрагмент встречи с кандидатом экономических наук, доцентом факультета экономических наук НИУ-ВШЭ, экономистом и политологом Алексеем Владимировичем Захаровым. Беседа на тему «Теория игр в изучении общества» состоялась 14 мая в Библиотеке-читальне имени И.С. Тургенева.

Полную видеоверсию лекции можно увидеть на канале «Полит.ру» в YouTube.

Петербургский школьник Данила Фиалковский вошел в число финалистов Всемирного смотра-конкурса научных и инженерных достижений Intel ISEF, который также известен под названием «малой Нобелевской премии», пишет «Интерфакс».

Данила Фиаловский стал участником российской команды в Intel ISEF после того, как в феврале победил во всероссийском конкурсе «Юниор» Национального исследовательского ядерного университета «МИФИ».

Петербургский школьник представил на конкурс исследование «Быстрый алгоритм вычисления коммутаторной длины в свободной группе». Ему пришлось соревноваться почти с двумя тысячами участников из 75 стран мира. В секции математики Фиалковский стал обладателем четвертой премии в размере 500 долларов.

В «Лаборатории непрерывного математического образования», в которой занимается школьник, рассказали, что награду ему вручили 15 мая в американском Питтсбурге.

Лауреат Нобелевской премии по экономике математик Джон Форбс Нэш-младший погиб в автомобильной катастрофе, сообщает ABC Newsсо ссылкой на полицию штата Нью-Джерси.

Согласно сообщению, Нэш и его супруга находились в такси, водитель которого не справился с управлением и врезался в парапет.

Джон Нэш получил широкую известность благодаря драме Рона Ховарда «Игры разума». В биографической ленте рассказывается о научных достижениях математика, а также его борьбе с шизофренией. Роль математика в драме исполнил Рассел Кроу. Фильм удостоился четырех премий «Оскар», в том числе в главной номинации – «Лучший фильм».

Джону Нэшу было 86 лет.

Лауреаты конкурса фонда «Династия» «Жизнь, посвященная математике» подготовили письмо в поддержку фонда.  Этот документ появился накануне конференции «Встреча поколений», которая пройдет 9–11 июня 2015 года в Независимом Московском университете (Большой Власьевский пер., 11). В ней примут участие победители конкурсов молодых математиков 2012-2014 годов и лауреаты конкурса «Жизнь, посвященная математике».

Мы рассматриваем решение Министерства юстиции признать иностранным агентом фонд «Династия», возглавляемый Д.Б. Зиминым, как беспрецедентную по своей нелепости акцию. Ни один частный фонд в России не сделал столько полезных дел для науки, образования,  просвещения, как фонд «Династия». 

Мы – профессиональные математики – могли бы привести целую серию тому примеров. Выдающийся конкурс фонда  «Династия» для молодых математиков – один из самых значительных конкурсов подобного типа в мире. Среди его победителей – самые талантливые молодые ученые, которые получили возможность работать в России благодаря стипендиям «Династии». 

Благородные акции фонда широко известны в стране, число его бескорыстных и благородных акций очень велико. Поэтому  решение Минюста есть проявление бюрократического безразличия к чрезвычайно важной, ценимой обществом и бескорыстной деятельности Д.Б. Зимина. Мы надеемся, что здравый смысл восторжествует, и это несправедливое и прискорбное по своим последствиям решения будет немедленно отменено. 

Лауреаты конкурса фонда «Династия»

«Жизнь, посвященная математике»

С.И. Адян, А.М. Вершик, Э.Б. Винберг, Л.Л. Максимова, Р.А. Минлос, В.М. Тихомиров

Публикуем стенограмму и видеозапись лекции Григория Анатольевича Кабатянского, доктора физико-математических наук, главного научного сотрудника Института проблем передачи информации РАН, профессора отделения прикладной математики и информатики НИУ-ВШЭ, с которой он выступил 13 марта 2014 года в рамках цикла «Публичные лекции «Полит.ру».

Текст лекции

Спасибо за приглашение, здравствуйте. Я постараюсь говорить понятно и увлекательно. Во всяком случае, предпосылки для увлекательного рассказа есть. Во-первых, коды, это что-то такое, что мы знаем еще из «Шерлок Холмса» Конан Дойля из его рассказа «Пляшущие человечки». А сегодня мы знаем это через Эдварда Сноудена и крики телевизора о том, что даже Ангелу Меркель подслушивают. Одна из целей моей лекции объяснить, что коды бывают разные, по крайней мере, три разных вида. Все они называются кодами.

Вторая интрига. Первым в названии лекции стоит Клод Шеннон. Мне  не повезло поговорить с ним лично – я начал ездить за границу в начале 1990-х годов, когда он был еще жив, но уже никуда не выезжал, у него была болезнь Паркинсона.  А мне очень хотелось познакомиться с гением. В своем интервью я сказал, что считаю его последним универсальным гением XX века. Интересно посмотреть на его судьбу. Когда он был школьником, то показывал всяческую одаренность, но он не был таким вундеркиндом как Джон фон Нейман или Норберт Винер.

Шеннона на Западе называют громким именем «отец цифровой эры». Некая  направленность  «в свое будущее» у него была с самого начала. Он, будучи подростком, сделал «беспроводной телеграф», чтобы общаться со своим приятелем, который жил в миле от него. Так что можно заодно его назвать отцом беспроводной связи. Некая интрига, которая кроется здесь, что, когда он учился, он получал, в свое время, степени бакалавра, магистра и PhD в математике и electrical engineering. Но американские математики его не признали. То есть когда вышли его работы конца 1940-х, то американцы его не признали.

Признали его советские математики. Начало этому положил Андрей Николаевич Колмогоров, которому его идеи очень понравились. Здесь мой рассказ близко примыкает к лекции Александра Шеня. Некоторые работы Колмогорова 1950-60-х годов были вдохновлены результатами Шеннона. А теперь я буду идти по слайдам, и постараюсь говорить, и не очень мучить вас математикой.

Здесь я написал, какие есть значения у слова «код». Одно – это «криптография», то есть, как написать ваше сообщение в таком виде, чтобы получатель мог прочитать, а никто другой не мог. Это нам всем  так или иначе знакомо. У Шеннона есть  основополагающая работа 1949-го года «Теория связи в секретных системах», на самом деле, она написана в 1945-м году или раньше. Это был такой отчет. Во время войны Шеннон работал, естественно, на оборонку, рассекретили этот отчет через четыре года. Как любят писать,  эта работа Шеннона превратила криптографию  из искусства в науку. Здесь, пожалуй, единственное место, где он предмет не «дожал». Он мог бы пойти и дальше, через сложность вычислений,  он это очень хорошо понимал, но остановился на некоем красивом математическом месте и дальше не стал развивать эту науку.

Второй значения слова «код» – этот  средство экономного представления («сжатия») информации. Из прежней жизни для нас такой пример - это азбука Морзе. Из сегодняшней: когда мы что-то архивируем на своем компьютере, то мы чаще всего пользуемся кодом  Зива-Лемпеля-Велча или какой-то его очередной модификацией. Начало этому положил опять-таки Клод Шеннон в эпохальной работе «Математическая теория связи» 1948-го года. Там он, в том числе, доказал теорему о потенциальных возможностях «сжатия»  информации. Насколько мы можем сжимать информацию при условии, что мы хотим ее точно восстановить. Он пошел дальше: а что, если мы хотим восстанавливать «почти» точно?

И третье, что мне ближе всего, это «код  как средство обнаружения и исправления ошибок при передаче информации или при ее хранении». Поначалу люди хотели, чтобы и при обработке можно было исправлять ошибки и их обнаруживать. И были такие попытки при исправлении ошибок в работе сумматора, но оказалось, что для этого дела коды не очень хорошо приспособлены. Но код «с проверкой на четность» – это то, что было  уже в самых первых вычислительных машинах (ЭВМ). Машины были огромные и очень ненадежные.

Это потом окажется очень полезным для возникновения теории кодирования. К информации из 7 бит добавлялся 8-ой бит так, чтобы целиком в этих 8-ми битах число единичек было четное (это и есть проверка на четность). Поэтому, если в ЭВМ происходила одна ошибка, то вы исправить ее не могли, но, по крайней мере, видели, что ошибка произошла. И вот в таких древних машинах звучал сигнал тревоги, и когда я учился на военной кафедре в МГУ, то даже такую машину видел, и ее «кормили» перфокартами.

Видеозапись лекции:

Это три темы, о которых я сегодня хочу рассказать. Давайте начнем по порядку, с Шеннона и криптографии. Есть теорема Шеннона, которая называется теорема об идеальном шифре. Она и написана на слайде, там объяснено  что такое «одноразовый блокнот».

Много пропущено в этом слайде. Вы хотите обменяться информацией с другим человеком. Здесь есть два разных подхода. Первый подход, что у вас уже есть некая общая секретная информация, которую знаете только вы, и не знает больше никто. Это та задача, которую рассматривал Шеннон, поскольку во время войны он работал в области криптографии. И это то, что больше всего любят в военных приложениях. Есть общая секретная информация, которая называется «ключ», и, с помощью этого ключа тот, кто посылает, превращает имеющееся сообщение во что-то другое, что приемник получив, может снова восстановить исходное сообщение, а вот все другие должны ничего не узнать о сообщении из того, что они перехватят по каналу.

Простейший такой способ,  и он здесь описан, называется «одноразовый блокнот». Выглядит он так: информация у нас записана из «0» и «1», это наши сообщения, которые мы хотим передать. Ключ – это случайная последовательность из «0» и «1», но одинаковая в том смысле, что случайно одинаковая и у меня, и у того, кто получает информацию. Например, какое-то физическое устройство ее породило, «0» и «1», независимо друг от друга появляются с вероятностью 1/2.

Мы эту информацию записали, и каждый у себя ее положил в карман. Это, конечно, недостаток. Если вспомнить старые книги о шпионах, то у шпиона обязательно был томик кого-нибудь, в зависимости от того, откуда он был или в какой стране он жил, томик Пушкина или томик Гейне, и надо было просто в соответствующий день открыть соответствующую страничку, это и был ключ, который там написан. Ну а потом, когда приходили его брать, то смотрели книжку, которая наиболее часто читалась. То есть частое чтение книг тоже бывает вредно для делаJ.

Кодирование или шифрование состоит в том, что мы складываем сообщение и ключ, которые у нас есть. Мы складываем «0+1=1», «0+0=0», «1+1=0», чтобы остаться в системе нулей и единиц. Тогда у нас получится некая новая последовательность нулей и единиц, и она передается по каналу. Тому, кто получает, просто: он достает бумажку из кармана, на которой написана  последовательность-ключ, и снова складывает с тем? Что пришло из канала. Складывает  по модулю «2», как говорят математики. То есть, когда один плюс один равно нулю. Вначале мы к сообщению  прибавили ключ, поэтому, сложив второй раз, мы его убрали, так как «1+1=0». То есть, по модулю два что сложить, что вычесть, - это одно и тоже. Если бы мы хотели строить такую же систему для десятичного алфавита, то надо было бы ключ вычитать (но по модулю 10). А здесь мы просто складываем. С легальным пользователем все просто, он, действительно, взял, сложил и получил наше сообщение.

Почему никто третий ничего не узнает о содержимом сообщения, не зная ключа? Я постараюсь это объяснить. Эти сообщения живут на трехмерном кубике, состоящем из нулей и единиц. Если это поможет представить. Это трехмерный кубик, у него восемь вершин, на них написаны «0» и «1». Наш ключ – это случайная последовательность, то есть если мы хотим что-то передать, то случайно выбираем точку на кубике. Поскольку кубик трехмерный, то я получу три бита информации, и сложу их. Все точки для меня одинаково устроены, я любую из них выбираю одинаково вероятно, значит, с вероятностью 1/8. Я выбрал, и теперь складываю со своим сообщением. Но сложение с сообщением означает, что картинка, которая у меня была на кубике (там стояли точки с приписанными вероятностями), теперь подвинулась.

Если бы картинка была бы неравномерной, например, если бы  нули появлялись  с вероятностью 0.99, зато  единички появлялись бы с вероятностью 1/100, то при такой «подвижке»  мы  бы все сразу увидели. Но здесь все точки одинаково вероятны, поэтому, подвинув картинку, она остается той же самой.

Это означает, что на выходе канала нелегальные пользователи видят одну и ту же «картинку», независимо от передаваемого сообщения. Они видят случайно появляющиеся последовательности последовательность из нулей и единиц. И это никак не зависит от того, с чем это складывалось. Это первая часть теоремы Шеннона, которая говорит, что одноразовые блокноты – это идеальные криптосистемы. Говоря на языке теории вероятностей, это означает, что апостериорная вероятность равна априорной, то есть мы ничего не узнали.

Вторая часть теоремы Шеннона несколько более сложная, она говорит, что если мы захотим сделать  так, чтобы ничего о сообщении не узнавалось, то лучше, чем этот одноразовый блокнот, мы не сделаем. Это будет означать, что длина ключа должна быть не меньше, чем длина сообщения.

Почему называется «одноразовый блокнот»? Мысль простая. Мы написали этот ключ на листке блокнота. Использовав его, вы листочек отрываете и выбрасываете, возможно, пропускаете через шредер. В статье википедии про одноразовый блокнот написано, что все знали, что его надо использовать именно таким образом. Но после войны советские шифровальщики все-таки использовали ключ несколько раз, и поэтому их сообщения удавалось раскрывать. Понятно, что будет плохого, если я один и тотже ключ использую два раза. Я получу одно зашифрованное сообщение Х,  затем другое сообщение Y,  сложу их. Ключи, как я говорил, уничтожатся, и я получу сумму сообщений «М + М’». Я не могу получить ни одно из сообщений, но сумму я их знаю, это уже довольно много.

Но что делать, если у нас нет общего «ключа»? Эту задачу Шеннон почему-то «пропустил», может быть, потому что он был математиком и инженером в одном лице, и он не решал задач, которые не стояли « в повестке дня». Но буквально через 15-20 лет появляются первые компьютерные сети,  в них  много пользователей и люди начинают понимать, что общий ключ это очень неудобно. Тогда и была придумана так называемая, public key cryptography, то есть криптография с открытым ключом. Современная криптография живет, в основном, в этом мире. То есть криптография с секретным ключом, иногда ее называют ее традиционной, в стиле Шеннона, все еще существует, но после Шеннона там особенно нечего было делать. У него было такое свойство  «закрывать задачи».

Когда говорят, что «Шеннон – отец цифровой эры», это не совсем точно, там есть и другие «отцы», но точно, что он единственный отец теории информации. «Теория современной информации вышла из его головы как Афина Паллада в полном боевом облачении», – так написано в одной статье о математической теории связи.

Многие вещи, которые Шеннон сделал, теперь общие для инженеров, для инженеров с математическим образованием, просто для математиков. В частности, это принцип блочного построения системы. Он говорил так: допустим, мы хотим передавать сообщения по каналу связи, мы хотим это делать надежно и быстро. Давайте разобьем эту задачу на подзадачи. Первая подзадача:  информацию мы хотим передавать эффективно, то есть затратив поменьше бит. Поэтому давайте  мы для начала представим информацию экономно, настолько экономно, насколько можно. А после того, как мы ее экономно представим, давайте мы ее будем передавать так, чтобы мы могли бороться  с помехами, которые есть в любом реальном канале.  Это уже будет вторая подзадача. Кстати, на русском языке есть классическая книга «Борьба с помехами», это редкий случай, когда русский язык звучит более выразительно, чем английский. Ну а если мы захотим, чтобы нас не подслушали, то это будет уже третья  подзадача.

Шеннон предложил  вероятностную модель описания сообщений. Допустим у вас есть газетный текст, но что с ним делать, как описать его закономерности? Есть алфавит, есть буквы, знаки препинания, как это все поместить в одну математическую модель? Он предложил делать это понемногу, по кусочкам, начать с простой модели, когда есть множество сообщений.

Будем называть их буквами, и пусть их М штук. И простота модели состоит в том, что у нас нет никаких связей между буквами, которые всегда есть в языке, то есть мы предполагаем, что буквы появляются друг от друга независимо с фиксированными вероятностями. Дальше мы хотим эти буквы записать в двоичном виде. Нужно взять последовательность из нулей и единиц, и не ограничивать себя, сразу решить, что последовательности могут быть разной длины, как в азбуке Морзе.

Дальше мы довольно хорошо понимаем, что мы должны делать. Буквы, которые появляются часто, им нужно ставить в соответствие короткие последовательности из нулей и единиц. Ну а буквы, которые появляются редко – на них уже, что останется. Вопрос, что останется? Это называется однозначное декодирование: если мы получим теперь последовательностей из нулей и единиц, то мы должны  суметь ее «разрезать» на куски, и однозначно установить, какие же там были буквы.

Шеннон сразу предложил такой способ однозначного декодирования – префиксные коды. Когда мы каждой букве ставим в соответствие слово из нулей и единиц, а эти слова обладают тем свойством, что ни одно слово не является началом другого. Тогда понятно, как нам нужно «резать» нашу выходящую ленту из нулей и единиц. Мы берем и смотрим, начиная с первых двоичных символов (битов), которые появляются, а вдруг это уже слово из нашего словарика, слово из нулей и единиц? Если нет, то добавляем следующий бит и т.д. Когда появилось первый раз слово-буква, то мы эту последовательность из нулей и единиц от общей последовательности отрезаем. Продолжаем «отрезание» дальше. 

Ясно, что этот процесс однозначный, если бы кто-то пришел и сказал, что это другая последовательность букв, то мы бы ему ответили: как же это может быть другая? Давайте посмотрим на вашу последовательность, какая у вас первая буква? Если соответствующее ей двоичное слово  длиннее слова для нашей первой буквы, то этого не может быть, потому что тогда наше слово является началом вашего. А если же оно короче слова для нашей первой буквы, то опять невозможно, потому что теперь  ваше слово является началом нашего.

Шеннон не стремился к сложности, он брал простые модели и на них сначала все понимал. Вот и в данном случае, после того как он предложил префиксные коды стали говорить,  что может быть это не единственный способ  кодировать-сжимать сообщения? И оказалось, что таких способов намного больше. Но для всех них верно то же самое неравенство Крафта, которое верно для простых последовательностей. 

Исходя из этого, Шеннон доказал следующую теорему. Как бы мы ни кодировали буквы, но к каждой буковке мы ставим какое-то двоичное слово. У этого слова есть его длина. И тогда мы понимаем, что нас интересует то, что называется средней  длиной буквы. Эта средняя длина и есть тот параметр, который мы хотим минимизировать. И первое, что он доказал, что среднюю длину однозначного кодирования нельзя сделать меньше, чем энтропия источника.

Здесь появилась знаменитая формула, что энтропия источника это сумма  логарифмов величин, обратных к вероятностям появления букв источника. И эта теорема Шэннона говорила инженеру, что как ни старайся, но «сжать» источник до средней длины, меньше чем энтропия, не получится. С другой стороны, он тут же предложил некий асимптотически оптимальный способ кодирования,  у которого средняя длина  стремится к энтропии источника, если вы будете кодировать выход источника не по одной букве? А сразу по многим. А именно, если кодировать побуквенно, то можно достичь энтропию «+1». А вот если вы будете от своего источника сообщения собирать слова какой-то большой длины, то там будет стоять та же самая энтропия "+1", но поделенная на длину слова, то есть «излишек» будет стремиться к нулю. То есть можно подходить все ближе и ближе к энтропии как только вы рассматриваете все более длинные слова.

Здесь уже появляется Андрей Николаевич Колмогоров. Он задал естественный вопрос. Всё, что делалось в работах   того времени  делалось в предположении, что статистика источника известна, в том числе, был придуман  написали оптимальный код Хаффмана. Колмогоров спросил, а что делать, если мы знаем, что источник такой, что у него буквы появляются независимо, но мы не знаем, с какими вероятностями. Я думаю, что Андрей Николаевич знал и ответ, и как его получить, но оставил задачу для других, для учеников.

Результат оказался удивительным, что можно сжимать информацию почти также хорошо, как если бы мы знали статистику. Конечно? Можно было бы воспользоваться примитивным подходом – понаблюдать источник сообщения, оценить вероятности букв, а затем использовать  код для полученной статистики. Оказалось,  что можно этого не делать, а  построить так называемое универсальное кодирование, которое осуществляет очень экономное сжатие информации в целом классе источников, и мы при этом не заботимся о том, чтобы знать, какое  распределение  вероятностей было реализовано.

То есть, если мы знаем статистику источника, то у Шеннона получалась энтропия «+1» поделить на длину тех последовательностей, которые мы забираем из источника. А в универсальном кодировании « излишек» вырастет  в логарифм раз. Конечно, это побольше, но не намного. Первое продвижение в этой задаче было получено Фиттингофом, потом значительные усовершенствования внесли  Р.З. Кричевский, Ю.М. Штарьков, Б.Я. Рябко, а на Западе – Т. Ковер и изобретатель арифметического кодирования Дж. Риссанен

Юрий Михайлович Штарьков, сотрудник ИППИ РАН, недавно написал замечательную книгу на  тему универсального  кодирования. Есть и другие приложения универсального кодирования, не только сжатие информации. Так, в криптографии очень важным является вопрос о том, насколько «случаен» тот или иной датчик псевдослучайных чисел. Борис Яковлевич Рябко, ректор Новосибирского университета телекоммуникаций, первым предложил использовать для тестирования алгоритмы универсального сжатия. А именно, если выход датчика можно заметно сжать, значит датчик не очень случаен (обратное, вообще говоря, неверно).

Следующее приложение еще более любопытное – атрибуция литературных текстов. Здесь работает следующий естественный подход: берутся разные авторы, берутся их тексты, и сжимаются. И оказывается, у разных авторов разная степень сжатия. Это особенно любопытно, если на вход такой программы запускать текст, который состоит из двух разнородных текстов: один текст от одного автора, другой текст от другого автора. Текст идет, и программа говорит, что это все один и тот же автор, потом затихает на время и говорит, что пошел другой автор.  Даже полнометражный документальный фильм сняли «Шекспир против Шекспира»по идее профессионального математика М.Б. Малютова.

 Это на самом деле  это очень популярная вещь и в теории вероятностей, только под названием задача о разладке, когда мы хотим находить момент перехода с одного распределения вероятностей на другое. Приложений тут очень много, например, отток клиентов из банков или если кто-то украл карту, меняется стиль того, что он покупает, с какой частотой он покупает и т.д. То есть мы хотим понять, что что-то «не то» произошло. Еще это все очень близко к предсказательному моделированию – есть на Физтехе  лаборатория Премолаб, созданная в рамках мегагрантов, которая всем этим, в том числе, занимается.

Слушатель: В кодировании используются простые числа для шифрования. Как они там используются и почему нужно очень большое число, чтобы расшифровать?

Г.К.:Действительно, я обмолвился, что была открыта криптография с открытым ключом, и люди получили за это престижную премию. Там было две группы: одна группа из двух человек придумала, как распределять ключи с помощью логарифма в конечном поле, а другая – систему шифрования, основанную на том, что разлагать целое число на простые множители видимо (это не доказано) вычислительно очень сложно. Вторая система, известная как RSA (Ривест, Шамир, Адельман), до сих пор очень популярна на практике.

В этой системе  открытый ключ порождается как произведение   двух больших простых числа (если числа маленькие, то систему тут же сломают),  а простые числа держатся в секрете!  Открытый ключ знают все, как и то, что он получен как произведение двух простых чисел. Жизнеспособность системы до сих пор базируется на том, что мы не знаем простых алгоритмов разложения числа на простые множители. Алгоритмы, которые мы знаем, имеют почти экспоненциальную сложность, то есть не допускают практическую реализацию в случае больших простых чисел.

Слушатель: Как по Шеннону определить информацию, как по Шеннону определить энтропию? Можно ли связать это математически? Потому что понятие энтропии столь многогранно, столь расплывчатое, понятие информации столь расплывчатое. Примерно сотни определений есть. По Шеннону, если две формулы написать и связать их?

Г.К.: На самом деле, определение – здесь, вот энтропия (показывает на слайды). Что сделал Шеннон, он четко указал границы, где это применять. У него в избранных трудах, переведенных на русский в начале 1960-х годов под редакцией Р.Л.Добрушина, есть статья «Теория информации и общий вагон». В каком-то смысле Шеннон протестовал против того, чтобы с помощью определения, которое он дал, мерили всё, что угодно. То есть он дал математическое определение: если у вас есть простой источник сообщений, то энтропия вычисляется так. Будет у нас другой источник, например,  текущий символ будет зависеть от нескольких предыдущих  символов, на три символа, тогда нам нужно будет подкорректировать определение. Прежде всего, это определение для вероятностных моделей.

Это не определение энтропии в физике, и не определение  смысловой информации, которую мы можем получить из текста (не думаю, что такое определение возможно). Александр Шень в своей лекции объяснял, что задача понять, сколько в данном содержится информации, – это не очень четко поставленная задача. Можно попытаться  придать ей  какой-то смысл, и вот Колмогоров его придал.

Он сказал, что текст или последовательность, это все одно и то же. Его сложность, то есть информация – это длина кратчайшей программы, которая его породит. А дальше начинается: на какой машине вы это делаете? И т.д. Колмогоровская сложность определена с точностью до константы. А здесь, у Шеннона,  еще раз хочу сказать, ответ простой. Шеннон определил это для вероятностных источников.

Борис Долгин: Вы сказали о том, что Шеннон был склонен закрывать вопросы. В какой степени он же и открывал до того? Или это были ответы на чьи-то вопросы?

Г.К.: Думаю, что в повседневной научной жизни, когда уже процесс пошел,   Шеннон ставил задачи себе и кругу своих учеников. У него, кстати, было много учеников, и они все превратились в хороших ученых. Но первоначальный импульс у Шеннона, как мне кажется, был из практики. Он видел задачу и решал ее.

Борис Долгин: То есть он, скорее, инженер в этом смысле?

Г.К.: В этом смысле да. А куда мы запишем Гюйгенса? Масса ученых занималась инженерными задачами. Гюйгенс разрабатывал маятниковый механизм для часов и его классический труд по механике  называется «Маятниковые часы». Нужно понимать, что математика стала профессией только в XX веке. Еще у Гильберта были ученики-любители. Еще пример: это основатели и первооткрыватели математического анализа Ньютон и Лейбниц. Про Ньютона более-менее знают, что он закончил жизнь главой Центробанка Великобритании. Но он собирался стать священником, так и поступал в Кэмбридж. Если посчитать суммарный объем того, что он написал про религию и про математику с физикой, так религии будет больше. Но это еще можно понять и принять.

А вот с Лейбницем, если вы не знаете, то никогда не догадаетесь. Лейбниц окончил университет в 19 лет и хотел получить искомую степень, а ему не дали, сказав, что в этом возрасте эту степень так рано не дают. Тогда он стал искать по Германии, и нашел университет, который ему дал степень по этим наукам. Что же это были за науки? По этой специальности он всю жизнь и проработал. Это была юриспруденция.  Она его, в основном, и кормила.

А все остальное он делал свободное от работы время. Может быть, мы именно к этому и идем с реформой науки и образования?!

Давайте продолжим. Дальше пойдет «надежная передача информации». Это была наиболее неожиданная вещь. Например, если вы говорите по телефону, и вас плохо слышно, то что вы делаете? Вы начинаете либо повторять всю фразу, либо вы каждую проговариваете буковку "'b' as in 'Bob'". На самом деле, это и есть простейшее кодирование. И этот способ повторения, в том или ином смысле, раскладывания буковки на много букв, он надежный, но нехорош тем, что вы снижаете скорость передачи по вашему каналу. Вы повторили три раза, и вы, тем самым, снизили способность передавать слова (информацию) в 3. И вот что оказалось неожиданно и с математической, и с инженерной точки зрения, что можно передавать информацию со сколь угодно малой вероятностью ошибки и при этом скорость передачи информации падает лишь в константу раз!

Я для примера рассматриваю такой простейший канал, он называется ДСК. Это двоично-симметричный канал, в котором символы искажаются друг о друга независимо с вероятностью p. То есть «0» может перейти в «1» с вероятностью p, «1» можете перейти в «0» с вероятностью p. С вероятностью «1-p» они передадутся без ошибок. И вот мы хотим передавать по такому каналу.

Если p=1/2, то мы ничего передать не можем, потому что появится «белый шум» и «одноразовый блокнот», как я уже сегодня говорил., значит, мы искажаем наш символ на выходе. То есть,  при p=1/2 мы складываем то, что мы передали в канал с последовательностью, в которой нули и единички появляются равновероятно, но это рассказанный выше «одноразовый блокнот».   

И мы уже убедились, что выход не  зависит от входа, то есть, чтобы мы не подавали на вход, выход будет один и тот же. Поэтому мы понимаем, что p должно быть меньше 1/2. Теорема Шеннона звучит так, что для любого сколь угодно маленького e >0 существуют такие способы передачи сообщений со скоростью передачи, меньшей пропускной способности канала C, что вероятность ошибки не превышает e. Если скорость передачи < C, то вероятность ошибки будет стремиться к «0» при росте длины сообщения, и наоборот.

Если мы захотим передавать со скоростью больше, чем пропускная способность данного канала, то вероятность ошибки будет отделена от нуля. Там будет какой-то порожек для вероятности ошибки, и что бы мы ни делали, мы ниже его не опустимся. В качестве примера, пропускная способность двоично-симметричного канала равна 1-h(p). Если мы вернемся к определению энтропии, то для p=1/2  получим h(p) =1/2 log2 + 1/2 log2, и формула в этом случае говорит правду, что здесь пропускная способность «0». Если только мы сделаем p меньше 1/2, то можно надежно передавать информацию, и даже видно, с какой скоростью можно это делать. Шеннон доказал эту теорему не  только для такого простого канала, а для целого класса каналов, и связал это с некоторой экстремальной задачей.

С точки зрения математики существование  такой константы С это тривиально – надо взять в качестве С верхнюю грань те скоростей, для которых такая передача возможна. Нетривиальность этой теоремы Шеннона в том, что она говорит как надо вычислять С (через энтропию).     

Это и  является главной математической частью теории Шеннона. Первым, кто признал его работы, был А.Н. Колмогоров. Он с удивлением рассказывал, что когда он говорил американским математикам о работах Шеннона, то они разводили руки, пожимали плечами, и не понимали, что там интересного, ведь он же не математик. Колмогоров спрашивал «Почему?», а они отвечали «он  теоремы не доказывает». Это тоже неправда, Шеннон доказывал теоремы. Я об этом расскажу ниже. Он, может быть, не доходил до каких-то деталей и тонкостей, но никаких ошибок у него не нашлось. А поле деятельности для математиков появилось огромное.

Я здесь написал, что потом теорему Шеннона о пропускной способности в более общих ситуациях доказывали  Хинчин, Колмогоров, Добрушин, Пинскер. И Добрушин, и Пинскер не просто работали  в ИППИ, а создали там атмосферу исследований. Понятие шенноновской энтропии вроде бы совсем простое,  тем удивительнее, что с помощью этого простого понятия  удалось доказать теорему пропускной способности.

Всё это подтолкнуло Колмогорова, по крайней мере, к трем замечательным открытиям. Построение нового инварианта  в эргодической теории, использование энтропии в задачах аппроксимации, и колмогоровская теория сложности. Это к тому, что не надо свысока смотреть на инженеров, тем более, если у этого инженера есть  еще и Ph.D. по математике, вдруг там что за этим кроется.

Теперь я расскажу немножко про коды, исправляющие ошибки. Я пропустил, что такое скорость передачи, не сказал, как исправлять ошибки. У Шеннона все это было, но было в таком странном виде, возможно, это послужило причиной отторжения у математиков того времени. Он доказывал, что существуют такие методы передач. Если бы он построил такой метод, наверное, не было бы такого отторжения. Но он же не так доказывал, так до сих пор и не умеют доказывать. А он говорил, что не предъявит конкретный способ передачи, но вместо этого предъявит класс способов передачи, и докажет, что, в среднем, они все хорошие.

Это означает, что вы можете из этого класса способов передачи вытащить любой, как фокусник зайца из шляпы, и он, с вероятностью, близкой к единице, окажется хорошим. То есть мы не можем предъявить какой-то очень хороший или очень плохой объект, но мы можем доказать, что все объекты, в среднем, вот такие. В математике считается, что этот метод изобрел Пауль Эрдёш, которого часто называли «Эйлером нашего времени». Но если посмотреть на даты, то Шеннон  сделал это раньше, а метод, конечно, тот же самый.

Еще из замечательных фактов про Шеннона: он написал магистерскую диссертацию, посвященную реализации Булевых функций на релейных схемах. То есть он написал, как строить элементную базу компьютеров, и как делать все простейшие операции. То есть фон Неман придумал архитектуру ЭВМ, а Шеннон – способ построения их элементной базы. Он показал, как реализовать эту схему.

После войны релейные схемы были безумно популярно, так как компьютеров еще не было, а  релейные схемы уже были, и люди делали на них разные устройства, которые реализовывали те или иные, теперь уже не непрерывные, как до войны, а дискретные функции. Возник вопрос, как сделать схему проще, чтобы там было меньше элементов. Было непонятно самое главное, что мы сможем этим добиться? Вот у нас есть Булева функция М-переменных, сколько нам понадобится этих элементов, чтобы эту Булеву функцию реализовать в самом лучшем случае, минимальной? И люди верили, что будет сравнительно несложно, что хватит какого-то полинома от числа переменных.

И вдруг Шеннон доказал, что нет, это минимальная сложность ведет себя как 2 в степени число переменных, поделенное на число переменных. Как он доказал? Вы думаете, он предъявил функцию, которая так плохо реализовывалась? И сегодня мы  не умеем этого делать, увы. Лучшее, что мы  умеем  доказывать,  так это квадрат от числа М переменных.

А Шеннон доказал свою формулу довольно просто. Каждой релейной схеме соответствует некоторый граф, а число его вершин и есть сложность реализации. Далее Шеннон сравнил число графов с данным числом вершин с тем сколько есть Булевых функций от М переменных ив се получилось! Такой трюки он придумал первым.  

А Хэмминг зашел с другой стороны, он дал первую конструкцию оптимального кода, который исправляет первую ошибку. У этого изобретения интересная история. В конце 40-х годов (прошлого века) Хэмминг занимался  численными методами и работал над атомным проектом. Вычислительные машины тогда были большие, ламповые и крайне ненадежные. Поэтому использовался простенький код с обнаружением ошибок, который, если что-то происходило, то выдавал сигнал тревоги. Если сигнал звучал, то тот кусок, где он прозвучал, запускали заново, с того момента, который записали. Но этот сигнал не работал по выходным, а Хэмминг по выходным много работал.

Когда он увидел, что результаты работы пропали, то стал думать, что если можно обнаружить ошибки, то почему бы их и не исправить. Он придумал первый пример, называемый теперь кодом Хэмминга, который породил целую науку под названием теория кодирования. Хэмминг написал книги и по численным методам, и по теории кодирования, но его лучшая работа - это статья на трех страничках 1950 года. В ней он не только построил код, но и ввел понятие двоичного пространства, которое также называется в его честь.

Это пространство последовательностей из нулей и единичек, а расстояние в этом пространстве определяется как число позиций, в которых две последовательности отличаются.  Американское научное общество IEEE присуждает золотую медаль им. Хэмминга (the IEEE Richard W. Hamming Medal) за лучшие работы в области теории кодирования. Из советских и российских ученых такую медаль получали Марк Семенович Пинскер и Владимир Иосифович Левенштейн. Первым получателем этой медали был сам Ричард Хэмминг. Я думал, что код Хэмминга это его основное достижение. Но нет, оказалось, что он еще  и основатель ACM – Ассоциации по вычислительной технике (Association for Computing Machinery).

Итак, код - это синоним произвольного подмножества пространства Хэмминга. Обычно нас интересует диаметр подмножества, то есть насколько далеко разбросаны его элементы. А здесь – нас интересует противоположная характеристика,  и мы спрашиваем, а как близко точки кода могут  подойти друг к другу. Минимальное из попарных расстояний и называется расстоянием кода. Слайд.

Код исправляет Т-ошибок тогда и только тогда, когда его расстояние больше, чем 2Т. Почему это так? Мы что-то передаем по каналу, это не произвольные последовательности из 0 и 1, а только последовательность из этого кода. Их миллион, или миллиард, мы их пронумеровали, и когда появляется сообщение с номером 537, то мы вытаскиваем его из кодовой книжки и передаем его в канал.

Почему мы можем исправить Т-ошибок, если минимальное расстояние больше, чем 2Т? Т-ошибок изменят слово в не более, чем Т-позиций, то есть кодовое слово – это начало, центр, а то, что получается в результате ошибок, это шарик в этой метрике радиуса Т. Другое кодовое слово – другой шарик радиуса Т.

Будет плохо, если шарики пересекутся, потому что в точке пересечения мы не будем знать, передавался один центр или другой центр. Но при этом условии шарики радиуса Т пересечься не могут, потому что у нас есть неравенство треугольника. Если расстояние между ними (центрами) 2Т+1, то шарики радиуса Т не пересекаются. Это равносильно тому, что код исправляет ошибки просто потому, что шары радиуса Т с центрами в словах кода не пересекаются.

На языке математики это означает, что нас в этом метрическом пространстве интересуют плотные, а лучше плотнейшие упаковки шаров. То есть как туда «напихать» побольше шаров так, чтобы они не пересекались? Дальше Хэмминг понял, что строить  произвольное множество с такими свойствами будет сложно, и решил ограничиться линейными подпространствами, рассматривая пространство всех последовательностей длины  n  как n–мерное векторное пространство над полем из двух элементов (поле вычетов по модулю 2). Тогда линейный код можно определить как множество решений системы линейных уравнений. Понятно, что если у меня всего N переменных, а уравнений R, то решений у меня будет 2 в степени (N - R), или больше, если среди уравнений есть зависимые.

Сам код Хэмминга устроен очень просто. Его длина выглядит как 2 в степени R минус 1, а показатель R - это число уравнений,   задающих код.  Матрица коэффициентов соответствующей системы линейных уравнений имеет  простой вид.  Ее столбцами являются  все двоичные векторы длины R, кроме чисто нулевого. Теперь понятно, что когда происходит одна ошибка, то вы берете принятое из канала слово, подставляете его в систему линейных уравнений, и то, что у вас получается в правой части, это в точности столбец, где произошла ошибка.

Собственно, Хэмминг сразу построил алгоритм декодирования, то есть исправления ошибок. Замечательная вещь в этом коде заключается в том, что если посмотреть на шарики, то они заполнят все пространство без дырок. Есть центр шарика, сама точка, и N-координат, по каждой координате можно изменить позицию. Значит, N плюс одна точка в шарике. Но N+1=2 в степени R. А решение у нас было 2 в степени N-R, вот все и сошлось. Мы заполнили все без дырок.

Такие упаковки называют плотными, или совершенными. Оказалось, что есть еще два совершенных кода, придуманных Голеем. Если работа Хэмминга 1950-го года, то работа Голея 1949-го года. О работе Хэмминга знали, она циркулировала, Голей уже опирался на нее. А Хэмминг не публиковал и ждал, пока получит патент – таким прагматичным был человеком. Когда он получил патент,  тогда и опубликовал свою статью.

Итак, есть два замечательных кода Голея, двоичный и троичный. Удивительная вещь, что хорошие конструкции используются не раз и возникают не раз и в математике, и в жизни. Оказалось, что троичный код до Голея придумал какой-то финн (извините, забыл фамилию), который  хотел выигрывать в «спортлото» по  угадыванию результатов футбольных матчей.  Там важен не счет, а только результат матча:  0 – ничья, 1 – проигрыш, -1 – выигрыш. Его интересовало, какие результаты поставить  в таблицу исходов так, чтобы покрыть все пространство возможных результатов с точностью до возможно неправильного угадывания двух матчей. Оба кода Голея востребованы в математике, потому что с их помощью проще всего построить известную решетку Лича и связанные с ней огромные простые группы. Отмечу, что  в начале 1970-х было доказано, что других совершенных кодов нет – результат, которым теория кодирования может гордиться.

Удивительная вещь: какие-то простые, на первый взгляд, вещи, долго не решаются. Люди доказали, что шариками радиуса 2,3,4 и т.д. нельзя плотно запаковать пространство, кроме двух кодов Голея. А про шарики радиуса 1 неизвестно. И здесь такая странная вещь: казалось бы, при чем здесь теория чисел? Она здесь вылезает. Есть гипотеза, что таких плотных упаковок нет, если алфавит нашего кода не равен степени простого числа. Если же он степень простого числа, то из алфавита можно сделать конечное поле и применить обобщенную конструкцию  Хэмминга.

И, наверное, последняя тема, связанная с кодами, это коды в дискретной геометрии. Одна из моих идей  данной лекции состоит в том, что обмен между чистой математикой и прикладной математикой – это не движение в одну сторону. Представление, что люди из чистой математики приходят в прикладную, решают задачу и уходят, неверно. Так, математические задачи приходят с другой стороны, со стороны приложений. Если посмотреть на историю математики, то есть периоды, когда новые задачи возникали не только из «внутреннего» математического любопытства; но есть и обратные периоды, как, например,  Средние века, когда основные математические достижения были мотивированы именно приложениями. 

Есть и другое движение – когда прикладная математика привносит новые идеи в «чистую» математику.  Как связать коды и дискретную геометрию? Давайте сделаем очень простое преобразование. Допустим, у нас есть двоичные коды, последовательности из «0» и «1» длины N. Давайте «0» заменим на «1», а «1» заменим на «-1». Тогда коды «переедут» из Булева кубика на сферу с центром 0 в евклидовом пространстве. Следующее очевидное  соображение – как посчитать скалярное произведение между евклидовыми векторами через расстояние Хэмминга.  Получится, что оно равно  N–2D, где D – расстояние Хэмминга.  

Если мы построили хороший код, то он дает нам какое-то хорошее расположение точек в пространстве. Оказалось, что если технику, которая уже была развита в теории кодирования,  применить к задаче о плотной упаковке шаров в евклидовом пространстве, то можно улучшить то, что в математике стояло так долго и незыблемо.

Что же именно? Мы упаковываем шары одного радиуса в n–мерное пространство, и смотрим, какая доля заполняется. Задача про упаковку трехмерного пространства, известная под названием гипотеза Кепплера, решалась четыреста лет, и была решена десять лет назад. Там, кстати, тоже были использованы идеи из теории кодирования как один из инструментов. Но я сейчас говорю не про трехмерное пространство, а про многомерное, я хочу понять,  насколько там можно плотно упаковать шары. Зачем это нужно? Например, точки в n–мерном пространстве – это сигналы для телекоммуникаций. Когда мы их «рассовали» далеко друг от друга, это хорошо, значит, сигналы не перепутаются.

Были известны следующие оценки, я тут написал, их можно чуть улучшать, экспоненты написаны правильно. Доля, которую мы заполним в пространстве наилучшим образом она не меньше, чем 2 в степени -N, это граница Минковского. А сверху мы не можем сделать плотность больше, чем 2 в степени -N пополам. Это оценка Блихфельда начала XX века. И геометры верили, что верна оценка Блихфельда, так как она доказывается довольно сложно, а оценка Минковского получается на «раз-два».

А главное, оценка Минковского заключается в том, что если вы бросаете точки в пространство случайно, то как раз и получится плотность равная 2 в степени -N. Но поверить, что случайное бросание может быть плотным, нельзя. Это противоречит всему, что было накоплено до этого. Верхнюю оценку удалось уменьшить, ее «подвинули» с 0,5 до 0,6, и это был большой сюрприз для геометров. Но, главное, что у них и мозги «подвинулись». То есть в теории кодирования люди уже за 50 лет работы свыклись с мыслью, что случайное бросание это очень хороший способ порождения хороших упаковок (кодов).

Одна из гипотез состоит в том, что для двоичных кодов  асимптотически лучше не бывает (для недвоичных это неверно). Теперь это уже довольно популярная гипотеза и в геометрии, что, наверное, в асимптотике самая плотная упаковка будет вести себя почти как случайная.

Хочу закончить лекцию возвратившись к жизни Шеннона. Малоизвестная вещь, что он был везунчиком, что он попал в какой-то национальный парк с семьей, и оказался там миллионным посетителем. Естественно, местные газеты написали, что Клод Шеннон с семьей из Массачусетса стал нашим миллионным посетителем. Прошел день, и уже по всей Америке пишут, что изобретатель теории информации стал миллионным посетителем.

Еще он замечательно жонглировал. Есть история, что когда он работал в Bell Labs, ему подарили велосипед с одним колесом, как в цирке. Он сел на него и поехал сразу, а через пару недель он уже ездил по коридорам и жонглировал тремя шариками. Кроме того, что он был математиком, он, несомненно, был и инженером. Если посмотреть, то он придумал какие-то устройства, машинки, которые в Японии выпускали с радиоуправлением. Из больших вещей он придумал первый в современном мире компьютер, который играл в шахматы.

Также придумал и сделал мышку, которая находила выход из лабиринта. Это считается началом искусственного интеллекта. Она ходила, искала, у нее были некие правила, куда ей двигаться. Лекцию я хотел закончить тем, что Шеннон назвал ultimate useless machine. Оказывается, у него было замечательное чувство юмора.

Обсуждение лекции

Борис Долгин: Спасибо большое. Вопросы, реплики?

Слушатель: Спасибо за лекцию. Вопрос такой, сейчас атомные станции, космические корабли, самолеты в условиях радиации летают, из-за облучений возникают ошибки, сбои. Какие системы исправления ошибок применяются и пришли ли к единому мнению? Или американцы делают одно, японцы другое и т.д. Это первый вопрос, а второй вопрос: Шеннон, Колмогоров, а Сифоров,  что он сделал, цитируют его сейчас или нет?

Г.К.: На самом деле, оба вопроса про ИППИ. Первый, про радиационную устойчивость, он у нас уже где-то с год внутри института «гуляет», мы сотрудничаем с Зеленоградом на предмет того, чтобы предложить им новые корректирующие схемы, которые были бы устойчивы к ошибкам радиации. Радиация оказалась очень противной штукой и для вычислительной техники.

Теперь вы сразу спросили, делаем ли мы одно и то же или разное с американцами. В тот момент мы делали с американцами, к сожалению, разное. Американцы делали умно, а мы про это не думали. Они биты одного слова  на своей плате  разносили, то есть то, что в теории кодирования называется перемежением. Поэтому, если вдруг даже происходил радиационный «пробой», то  пробивалось в разных словах, в каждом слове появлялось по одной ошибке, и ничего страшного. А у нас биты одного слова лежали подряд, и поэтому портилось целиком слово, а это  может привести к сбою в работе ЭВМ.

Про Владимира Ивановича Сифорова… Говорят, что он был хорошим директором. Я у него никогда не работал, я работал в почтовом ящике, когда был молодым, и долго работал. Я ходил в ИППИ на семинары, так что  Владимира Ивановича видел, даже беседовал, потому что я собирал отчеты  для  Совета по кибернетике. Сифоров интересовался тем, что происходило в  тематике передачи информации. В.И. Левенштейн мне рассказывал,  как у него получилась первая печатная работа (ее потом американцы переоткрыли, и даже получили премию за эту работу, ну а потом извинялись, говорили, что они не знали– я не верю).

Так вот Сифоров на семинаре, это конец 1950-х годов задал следующий вопрос: «Я строил двоичный код следующим образом: выписывал подряд последовательности из нулей и единиц фиксированной длины, начинал с чистого нуля, хотел построить код, например, с расстоянием пять. И смотрел по словам, я смотрел первое слово, которое на расстоянии пять, выписывал его. Хорошо, потом начинал двигаться дальше по своему списку упорядочения, искал первое слово, которое от этих двух на расстоянии пять или больше. Как только находил, добавлял его к списку, и так далее. В примерах у меня всегда итоговый код – линейный. Это верно всегда?».

Это то, что теперь называют «жадным» алгоритм, и Владимир Иванович его первый придумал. 

Слушатель: На прошлой лекции Александра Шеня я вдохновился примером эксперимента с музыкой разных композиторов, где архивировали миди-файлы и складывали сумму, и сравнивали с архивом суммы. Сумма архива больше архива суммы. Это степень сжимаемости показывала похожесть. Вы сравнивали писателей, их похожесть, на Шекспира. Скажите, где об этом можно почитать? Хочется прийти домой и почитать об этом. 

Г.К.: Напишите Михаил Малютов по-английски, и вылезет куча всего, включая маленький телевизионный ролик, Малютов очень гордится, что его сняли, где он рассуждает, кто же и что  написал (Ред. "Шекспир против Шекспира" на телеканале "Культура"). 

Слушатель: Спасибо за лекцию. А можно чуть углубить или расширить вопрос? Вы упомянули изыскания г-на Малютова, в том числе по поводу кодирования и сжатия литературных текстов, и то, что можно четко отследить, что это текст одного автора, а потом другого. А вот что касается музыки, получается, что музыку тоже можно кодировать?

Г.К.: Если оцифровать, то да.

Слушатель: А что принимается за единицу музыки?

Г.К.: Здесь такая же ситуация, как с определением отцовства. То есть, если оказалось, что степени сжатия разные, то вероятнее всего  исполняли или писали разные люди. Но если степень сжатия примерно одна и та же, то это совершенно не означает, что писали одни и те же люди, это первое замечание. Что касается музыки, как последнюю похвалу Шеннону, если посмотреть, там есть четкий водораздел: до Шеннона все аналоговое, пластинки и т.п. И вдруг все перестроилось, все перешло на цифру, оказалось, что мы, если теряем что-то, то ухо это не слышит.

Откуда мы с вами будем брать музыку? Если это кассетная запись, то это проще простого, там есть алфавит, и его надо закодировать и сжать. Наверное, с этим способом можно было бы даже определять, а кто, собственно, играл. Если, наоборот, брать диск, там все равно уже все оцифровано, и сравнивать одно и то же произведение, как оно играется разными пианистами.

Слушатель: Скажите, а вот разницу между смыслом и информацией вы могли бы прокомментировать?

Г.К.: Это не ко мне, это к специалистам по онтологии. Правда, не знаю, это как раз то, от чего Шеннон старательно открещивался. Он не говорил, что там много смыслов, он говорил, что это нельзя коротко записать,  а есть ли  в этом смысл – он за это не отвечает. То есть информация – это тот минимальный объем, которым вы можете описать то, что вы хотите. А есть там смысл, нет – сегодня это только человек решает.

Наш директор, Александр Петрович Кулешов, любит  приводит  как пример то, что объем информации за последние год-два года  удваивается! То есть, за два года было порождено  столько же, сколько за всю предыдущую историю человечества.  Но это же не значит, что мы удвоили наши знания.

Слушатель: Если заархивировать?

Когда мы заархивируем, это станет  ближе к информации, в том смысле, например, что дубли почти исчезнут. Раньше люди стремились экономно записать, сжать, а сейчас нет таких проблем. Я до сих пор помню свой первый ноутбук, у него всей памяти было 8 Гб, и ничего, он работал. Сейчас бессмысленно об этом говорить, потому что никто не думает об объеме памяти , когда пишут программы. Ну иногда, когда задача требует экономить память...

Константин Иванович: Когда выступал Александр Шень,  то он сказал грустную вещь, что в МГУ на мехмате сейчас уже перестали преподавать теорию Галуа, ее знают только профессиональные алгебраисты. В вашем институте знают теорию Галуа? Понимают ее? Преподают ли студентам и используют ли в теории кодирования?

Г.К.: Хочется ответить языком того «почтового ящика», в котором я проработал половину своей рабочей жизни. Те, кому нужно, кто с ней работают, те и знают теорию Галуа. Добрушин очень любил приводить пример, что большая  часть математиков не знает, что такое конечные поля, как они устроены, а инженеры-связисты, оказывается, знают, так как им это нужно.

Слушатель: Вы сказали про отцовство, отсюда у меня и появился вопрос. Вы ни слова не сказали про генетический код.

Г.К.: Конечно, нет. Это отдельная тема. Я не говорил об этом, потому что, все мы читали Козьму Пруткова и знаем, что «нельзя объять необъятное». Да, есть генетический код,  и там  много задач, эти задачи  чем-то близки к теории кодирования, но, к моему удивлению, это не задачи теории кодирования. Современные математики эти задачи называют  комбинаторикой на словах. Но кодов там не оказалось.

 То есть, как Бог или кто-то исправляет ошибки в хромосомах, я не знаю, и  даже не хочу за это браться. Но могу  отметить, что кодов, исправляющих ошибки, в привычном понимании, чтобы это был хороший код, чтобы он был близок к оптимальному, на сегодня там нет. Мы часто думаем, что природа оптимальна. Вот сколько времени в бионике была идея о том, что нужно просто брать, копировать природу и все будет хорошо. Но в природе хорошего кода, исправляющего ошибки, по крайней мере, генетического кода, не оказалось.

Слушатель: Я – биоинформатик. Я сформулирую по-другому, есть два множества. Одно кодируется случайным образом и второе множество – случайным образом. Эти два множества складываются, и в результате получается единственно точный ответ. Чтоб было понятнее: ДНК матери кодируется самостоятельно, ДНК отца кодируется самостоятельно, эти процессы вероятностные. Не конкретно такие-то и такие гены, а в случайном порядке. Когда сливаются эти две клетки, получается ген, который имеет абсолютно четкое расположение, развивается нормально. Вы когда-нибудь видели такие множества, такой способ программирования?

Г.К.: Если в семье не один ребенок, так они что все одинаково устроены?! Получается другой ребенок, другая хромосома, другой набор.

Слушатель: Наборы одни и те же. Абсолютно точно говорю, достоверно.

Борис Долгин: Подождите. Генотипы двух детей одних и тех же родителей одинаковы?

Слушатель: Нет, генотипы родителей для этого ребенка и для другого одинаковы.

Г.К.: Я на этот вопрос не отвечаю, это не по теме моей лекции. Сразу скажу: я не буду отвечать на вопросы по биоинформатике, мне эта область очень интересна, но я в ней не специалист. Я отвечаю только на те вопросы, которые касаются моей области.

Слушатель: Даже если вы не ответите, этот вопрос должен прозвучать. Вы сказали, что хорошего кода для исправления ошибки не оказалось. Почему: нашли, что нет, или не искали?

Г.К.: Не знаю.

Слушатель: Спасибо за прекрасную лекцию, Григорий Анатольевич. У меня вопрос, связанный с развитием систем. Есть такие понятия: саморазвитие, самоорганизация и т.д. Возьмем нашу планету, я читал, что там, якобы уже 4 млрд. лет назад плавали одноклеточные животные. От этих простейших систем мы дошли до homo sapiens. Вопрос: поскольку математические формы – это тоже объективная реальность, и все, что вы сегодня рассказали и о кодах, и сжатии, о вероятностных, случайных процессах, все это происходит в природе, а не только в теории у математиков. Как в природе за эти 4 млрд. лет все эти математические кодирования, все эти свои каналы передачи информации, как это все осуществлялось?

Г.К.: Передача по каналам информации начинала осуществляться с Попова-Маркони, это сто с небольшим лет. Дальше, если это относится к живой природе, то я уже сказал, что это не моя тема. А передача информации в неживой природе – это , кажется, ничья тема.

Борис Долгин: На самом деле, в реплике-вопросе, который только что прозвучал, прозвучал некоторый полу-вопрос, по которому математики иногда самоопределяются. Это вопрос об онтологичности математики. Бывают платоники, неплатоники, те, кто думают, что это что-то, действительно, объективно присутствующее или что это все-таки чистые мыслительные конструкты, которые можно более или менее удобно использовать для описания тех или иных явлений. Хотите ли вы самоопределиться на эту тему?

Г.К.: Нет, я – прикладной математик.

Борис Долгин: Можете ли вы посоветовать какую-то литературу по теме? Предположим, вышли отсюда люди, которые впервые услышали о том, что вы рассказали, и захотели продолжить читать.

Г.К.: У нас в ИППИ есть самый старый сотрудник Юрий Львович Соколович. Ему практически 90 лет, в войну он был командиром взвода разведчиков, и только в этом году он перестал читать лекции. Пару лет назад, когда был некая вечеринка, люди пели песни, и другой немолодой человек говорит: «Юрий Львович, все не знают, но вы должны знать, была такая песня сталинских времен "Простое письмо", напомните слова». Он, опираясь на палочку, сказал: «А причем здесь я, спросите yandex!».

Борис Долгин: Какой смысл в моем вопросе, разумеется, можно посмотреть в поисковике. Но вы, как специалист, наверное, имеете какое-то представление о том, что является адекватным, что является лучшим. Что вы рекомендуете, читая лекции. Что бы вы рекомендовали, на ваш вкус?

Г.К.: Я скажу, но сразу поставлю ограничения. В теории кодирования есть, условно говоря, ее «Библия»  это книга Мак-Вильямс и  Слоена, русский перевод 1979 года, при этом, как и положено «библии», она почти не  устарела. Но это книга для математиков. Есть книга, которая больше про Шенноновскую теорию, про надежную связь, про сжатие, это книга Галлагера «Теория информации и надежная связь». Эта книга для математиков, которым интересны прикладные задачи, или для прикладников, которые достаточно хорошо знают математику.

Популярных книг на эту тему я не знаю. Когда-то была такая книжка в библиотечке «Кванта» Аршинова и Садовского «Коды и математика». Понимаете, как всегда, в популярной книге есть плюс в том, что ее можно читать, но есть минус в том, что, если в ней  нет ошибок, то это уже хорошо, но она все-таки дает несколько поверхностный взгляд на предмет. На английском языке книг гораздо больше, в том числе, и популярных, но переводить никто не хочет.

Наталия Демина: У меня вопрос по телекоммуникациям. Сначала было 2G, потом 3G, сейчас 4G, то, что вы делаете, связано с развитием этого?

Г.К.: Я больше теоретик, чем практик, и для меня мобильный телефон по-прежнему загадка. Почему он работает, почему они друг другу не так сильно мешают? Мое убеждение, что там, по существу, нет никаких новых возникающих теоретических задач. Но  есть постоянное улучшение уже существующих решений. Что-то меняется, будет 5G, увидим, что оно даст. На самом деле, если вы посмотрите, там всегда есть большая разница между тем, что обещается, и тем, что получается. То есть в Москве уже есть  LTE (4G), но реальная скорость передачи информация в разы меньше того, что обещается. Но, тем не менее, правда состоит в том, что связь постоянно улучшается.

Слушатель:Что вы заканчивали? Скажите о себе несколько слов.

Г.К.: Мехмат МГУ. Когда я там учился, я никакими кодами не занимался, там была некая история, почему я не остался в аспирантуре, может быть это и хорошо,  что не остался. Я вообще считаю, что Бог ни делает - все к лучшему. Когда я пришел в «почтовый ящик», то мой начальник вынес книжку со словами «Вот ты закончил кафедру алгебры, это очень хорошо, ты теперь  с этим разберешься и нам расскажешь». Книжка называлась «Алгебраическая теория кодирования» Э. Берлекэмпа.  Вот до сих пор продолжаю разбираться. 

Берлекамп – очень хороший математик. Из забавного – он  занимался играми и, в том числе, играл на бирже, но и здесь Шеннон – первый!  Более того, Шеннону принадлежит изобретение первого переносного компьютера. Шеннон его построил для игры в блэк-джек, и с ним он ездил в Лас-Вегас. Потом это превратилось в некую литературную историю, потом уже и в фильм. То есть в этом смысле Шеннон -  такой типичный американец, он везде видел деньги (ну там где они есть). А идеи, которые у него были в теории информации, они сейчас довольно популярны в математической экономике. Там есть «Универсальный портфель Ковера».  Но это тоже все по следам Клода Шеннона.

Слушатель: У вас почти вся лекция была посвящена кодам для исправления ошибок и для обнаружения ошибок. Что известно о попытках исправления и обнаружения вставки символа и потери символа?

Г.К.: Этим занимается мой старший коллега и товарищ Владимир Иосифович Левенштейн, он придумал в 1965 году то, что теперь называется метрикой (расстоянием) Левенштейна. Оно определяется как минимальное число вставок и-или выпадений символов, которые переводят одну последовательность в другую. То есть это такой аналог метрики Хэмминга для исправления как раз ошибок вставок, выпадений, но она изучена гораздо хуже, потому что сама метрика само по себе гораздо хитрее.

Объясню простую вещь, по которой сразу станет понятно, почему она хитрее. Там шары одинакового радиуса в разных точках имеют совершенно разный объем. Это понятно, вот у вас есть вектор из всех нулей, и пусть будет у вас выпадать пять символов в каких-то позициях. Что вы получите? Каждый раз  один и тот же вектор из нулей. А вот если у вас есть вектор, в котором половина нулей и половина единичек, и  они довольно хаотично разбросаны, то выбрасывая пять символов, вы получите кучу разных векторов. Там такая тяжелая для исследования метрика, и  хотя, как всегда, есть границы существования хороших кодов, но явных конструкций, за исключением кодов, исправляющих одну вставку, одно выпадение (а это сделал еще Левенштейн), реальных конструкций нет.

Борис Долгин: Спасибо большое! (аплодисменты)

Японский математик Синъити Мотидзуки согласилсяобъяснить своим коллегам выполненное им доказательство abc-гипотезы – одной из ключевых проблем теории чисел. Мы рассказывали об этом доказательствев 2013 году, когда с момента его появления прошло полгода, но другие математики так и не могли проверить, верно ли оно. За прошедшие с тех пор два года мировое математическое сообщество не добились особых успехов. Лишь четверо математиков объявили, что они разобрались в сформулированном Мотидзуки доказательстве и подтвердили его правоту.

Сформулированная в 1980-х годах abc-гипотеза устанавливает для тройки взаимно простых (то есть не имеющих общего сомножителя) чисел некое отношение между ними и произведением всех их сомножителей, возведенным в степень, большую единицы. Ее доказательство, если его удастся получить, многие математики считают одним из важнейших достижений века. Мотидзуки впервые объявил об успехе в 2012 году, через некоторое время коллеги смогли найти ошибку в его доказательстве, но японский математик ответил, что ошибка не влияет на конечный результат, а через некоторое время представил исправленную версию доказательства. Но с проверкой и признанием его работы возникли сложности. Дело в том, что Мотидзуки излагает свои доказательства весьма оригинальным и сложным математическим языком, создав новую область математики, названную им «арифметической теорией Тейхмюллера», и вводя множество новых понятий, например, «анабелиоиды», «Фробеноиды» или «театр НФ-Ходжа». Доказательство abc-гипотезы он представил в четырех статьях (1, 2, 3и 4), которые опубликовал на личном сайте. Общий объем их текста превышает 500 страниц. Позднее из снисхождения к математическому сообществу он вывесил там же «панорамный обзор» доказательства, но и этот обзор оказался очень сложен.

Теперь же Синъити Мотидзуки согласился дать комментарии по поводу своего доказательства в ходе конференции Математического института Клэя в Оксфорде, которая пройдет в декабре. Математик будет отвечать на вопросы коллег при помощи Skype, так как покидать Японию он не хочет. А в июле 2016 года запланирована конференция «Вершины арифметической теории Тейхмюллера» в Киото, где ожидается личное присутствие Мотидзуки.

В Чикаго было проведено исследование, которое показало, что дети, родители которых хотя бы раз в неделю перед сном занимаются с ними математикой, значительно опережают в освоении этой науки своих сверстников. По данным авторов исследования, за девять месяцев участвовавшие в нем дети опередили одноклассников примерно на три месяца. 

Подход работает даже тогда, когда родители не уверены в собственных математических способностях, и обычно не решаются обсуждать с детьми математику.

Когнитивные психологи Шан Бейлок (Sian Beilock), Сьюзан Левин (Susan Levine) и их коллеги из Чикагского университета привлекли к исследованию семьи 587 первоклассников из 22 школ Чикаго. Среди них были ученики частных и государственных школ, живущие в семьях с разным достатком. Родителям каждого ребенка дали планшетный компьютер, с которого надо было читать ребенку перед сном. Четыреста двадцать семей должны были использовать чтения текстовых задач, связанных с счетом, действиями арифметики, дробями, геометрическими фигурами и вероятностями, используя при этом специальное приложение Bedtime Math. Еще 167 семей использовали приложение для чтения. В начале и конце учебного года исследователи оценили математические знания всех детей при помощи стандартизированного теста.

Как оказалось, занятия математикой перед сном значительно ускорили ее освоение детьми. Те из них, чьи родители использовали приложение Bedtime Math два или более раза в неделю, опережали тех, чьи семьи делали это реже. Самое интересно, что эффект был заметен даже в тех семьях, где родители сами не любили математику и считали, что знают ее плохо.

Родители часто считают, что обучение математике должно быть задачей школьных учителей. «Мы надеемся, наше исследование поможет изменить мнение, что математика является прерогативой школы, и показывает, что разговоры о математике дома очень полезны», – говорит Бейлок.

Отчет об исследовании опубликованна сайте журнала Science.

Завершается прием заявок на конкурс для молодых математиков. Заявки принимаются до 15 октября 2015 года. Новый конкурс уникален тем, что он стал возможен благодаря личной поддержке Дм. Зимина, П. Делиня, А. Герко, А. Мурашова, А. Алиева и других благотворителей. Об этом сообщает Независимый московский университет.

Как известно, в 2015 году конкурс фонда «Династия» для молодых математиков завершился в связи с ликвидацией фонда. Лауреаты конкурсов 2012-2014 годов получают стипендии в соответствии с ранее объявленными правилами. Российские математики выражают глубокую благодарность фонду «Династия» и лично Дмитрию Борисовичу Зимину за многолетнюю поддержку российской математической школы. 

В связи с важностью конкурса для сохранения и развития российской математической школы, жюри конкурса и Независимый Московский университет приняли решение продолжить проведение конкурса, опираясь на поддержку частных благотворителей. Конкурс 2015 года будет проводиться по тем же правилам, что и конкурс фонда «Династия». Подробности на странице http://www.mccme.ru/dfc/.

На этой неделе в Москве, в Центре документального кино, состоялась мировая премьера научно-популярного фильма «Буквальная геометрия». Выпускница физико-математической школы, режиссер Екатерина Еременко, автор фильмов «Мой класс» и «Чувственная математика», представила зрителям новую работу. «Для нас это азартная история. В фильме больше специй и больше математики, и мне будет очень интересно увидеть, готовы ли зрители к такому формату». 

В ее 66-минутном фильме, кажется, собрано всё лучшее из того, что того, что было в «Моем классе» и «Чувственной математике» – попытка визуализировать напряжение человеческой мысли, эмоций и страстей, связанных с наукой. Работа математиков показана не только как полет фантазии, как напряженный и непонятный широкой публике труд «психов»-фриков-одиночек, но и как работа команды, социальное взаимодействие, рождение идей в рамках формальных и неформальных встреч ученых, регулярного общения коллег по проекту и докладов ученых, приехавших выступить на семинаре. 

Трейлер фильма

Сюжет фильма построен вокруг большого проекта по дискретизации геометрии и динамики, возглавляемой математиком Александром Бобенкоиз Технологического университета Берлина. «Проект рассчитан на 12 лет, и это позволяет в двигаться в перспективном направлении в долговременном режиме. Финансирование составляет порядка 2 млн евро в год. Сейчас закончились первые четыре года проекта. В нашем центре («Дискретизации геометрии и динамики») работает порядка 60 человек, а в моей группе около 15 человек», – отметил Бобенко. 

Одним из практических приложений этого проекта стало создание нескольких павильонов на Эйфелевой башне с помощью теории конических сетей, придуманной профессором Технического университета Вены Хельмутом Потманом (Helmut Pottman). «Мне так повезло, что мы сняли математиков в касках», – смеется Екатерина. 

Обсуждение фильма в ЦДК, 13 октября 2015 года, часть 1. 

Обсуждение фильма в ЦДК, 13 октября 2015 года, часть 2. 

«Такое быстрое применение идей дискретной дифференциальной геометрии для меня самого стало неожиданностью. Обычно на это уходит лет 20, а тут прошло всего 5 лет от создания науки до павильона на Эйфелевой башне», – подчеркнул Бобенко. Режиссер фильма рассказала, что Хельмут в свое время хотел стать школьным учителем и преподавать рисование, но его на эту работу не взяли, и стал заниматься геометрией, а теперь Потман – признанный эксперт в области индустриальной и архитектурной геометрии. 

Появление Джона Нэша и Фримена Дайсона (Freeman Dyson) стало и изюминкой фильма, и несколько выбивающимся из повествования. Участвовали ли они в работе по проекту или стали своего рода «свадебными генералами»? Екатерина Еременко пояснила, что, по просьбе организаторов Абелевской премии, снимала короткие ролики про Нэша, и их научным консультантом выступил Александр Бобенко. Возможно, что видео с Нэшем, Нобелевским лауреатом по экономике 1986 года и Абелевским по математике 2015, трагически погибшем в автокатастрофе в мае 2015, станет основой для нового фильма. «Мы сохранили видео с разговором Дайсона и Нэша и этот материал пойдет в работу». 

«Оказалось, что про Дайсона почти никто ничего не снимал. Его снимал Стэнли Кубрик в «Космической одиссее», но потом вырезали. И японское телевидение пригласило Дайсона для съемок фильма о бабочках, где Нобелевский лауреат должен был сидеть в углу, думать и изображать ученого», – рассказала Екатерина. 

По ее словам, в «Буквальной геометрии» Нэш и Дайсон были важны для демонстрации иерархии в научном сообществе, что там есть свои культы личностей, свои боги и мессии, а также парадокса, что как аспирант, так и признанный мэтр могут испытывать сомнения в выбранном пути. В фильме показаны и молодой ученый, мучительно раздумывающий стоит ли ему оставаться в науке, сможет ли он выдержать конкуренцию, готов ли он отдавать все силы исследовательской работе, чтобы оставаться на высоте, и великие ученые, которые вовсе не считают себя примерами для подражания. «Я не совсем уверен, что я сам настоящий математик», – говорит в фильме Нэш.   

Александр Бобенко рассказал, что пригласил Екатерину к совместной работе, посмотрев ее фильмы о математике. Он дал ей полный карт-бланш в работе, но ученые не сразу привыкли к присутствию возле них режиссера. «Катя сидела в уголке и снимала, и сначала нас это очень раздражало, нельзя на это не обращать внимания, но потом мы привыкли». 

«С одной стороны, это было хорошо, что я так была тесно интегрирована в этот проект, но, с другой стороны, это было минусом. Когда ты приезжаешь как режиссер извне, то возникает эффект попутчика в поезде, которому раскрывают душу, и потом нужно очень бережно всё смонтировать и решить, что интимное использовать, а что нет. А тут, я никуда не уезжаю, а коллег не принято слишком близко к себе подпускать, напротив принято держать дистанцию, и для меня это стало вызовом, интересным режиссерским опытом», – отметила Екатерина. 

«А вам что-то новое открылось в вашем собственном проекте?», – спросила я Александра Бобенко. «Да, есть моменты, которые не вошли в фильм. Так, в ходе съемок мы решили, по просьбе Екатерины, обсудить, чем же мы занимаемся в этом центре. И мы поняли, что никогда этого раньше не делали. Мы никогда по-серьезному не обсуждали, куда мы движемся, куда идем. И мы пошли на полянку, и стали обсуждать, и это было очень полезно», – заметил Александр. 

Фильм заканчивается списком научных статей, созданных в ходе проекта, и задачкой для зрителей, которую, по словам режиссера, может решить даже 8-летний ребенок. Тем не менее, эту задачку, поставленную перед героями фильма (им был дан 1 час), решил только Александр Бобенко. 

Журналисты попросили еще раз объяснить условия задачи «вырезания печенюшек на тесте». «Представьте себе треугольники на плоскости, и их можно сдвигать параллельно в любом направлении, так чтобы треугольники не пересекались. Теперь вся площадь на плоскости делится на две области: которая лежит внутри треугольников и оставшаяся снаружи. Надо сделать так, чтобы площадь внутри треугольников была максимальной, а снаружи – минимальной. Какое отношение этих площадей? Кажется, что отношение будет половина на половину, но, на самом деле, это не так», – пояснил профессор. 

«Не кажется ли вам, что математика у вас в фильме победила кино?», – спросили Екатерину. – «Нет, я как раз использовала то, чему я научилась в кино, для очень сложной задачи. Показывать математику – очень сложная вещь. Что показывать? Как показать мыслительный процесс? Как оставаясь в области кино, показать сложную математику, увлечь людей эмоциями и страстями математиков? Это актуальная и сложная задача, которую я пыталась решить, работая над этим фильмом. Я использовала всё то, чему я научилась в кино, для рассказа о математике». 

На фото слева направо: Ирина Белых, Екатерина Хаустова (прокатчики, Фестиваль актуального научного кино), Александр Бобенко (математик) и Екатерина Еременко (режиссер фильма "Буквальная геометрия")

Надеюсь, что «Буквальная геометрия» найдет в России и других странах своего зрителя, а в Москве состоится показ фильма с последующей научно-популярной лекцией Александра Бобенко о математике. Очень хочется услышать от героев фильма более подробный рассказ об их проекте. 

Справка о фильме: Над фильмом работали: автор и режиссер Екатерина Еременко, операторы Игорь Морозов и Ирина Шаталова, ассистент режиссера Сергей Карпенко, режиссеры монтажа Павел Костомаров и Марат Магамбетов, монтажер Наталья Прохоренкова, звукорежиссер Артур Хайруллин, В фильме использованы кадры из учебного фильма Александра Бобенко и Чарльза Ганна "Conform!" и музыка Штефана Зехельмана. 

Главный научный сотрудник Петербургского отделения Математического института РАН Анатолий Вершикстал единственным российским ученым избранным в этом году в Европейскую академию наук (Academia Europaea). По словам математика, он ничего не знал о выдвижении до извещения из академии две недели назад. 

В Европейскую академию помимо Вершика входят несколько ведущих российских математиков: Сергей Новиков (избран в 1990), Альберт Ширяев (1990) и Людвиг Фаддеев (1989). В отделении информатики шесть россиян: Михаил Гельфанд (2010), Эдуард Гирш (2014), Юрий Матиясевич (2014), Николай Верешагин (2014), Виктор Зиновьев (2014) и Виктор Садовничий (избран в 1998). 

Математик Владимир Арнольд был избран в эту академию от Франции. Среди известных математиков, выходцев из России, но избранных от других стран: Яков Синай и Александр Бейлинсон – от США, Станислав Смирнов – от Швейцарии, Михаил Громов, Максим Концевич и Юрий Кабанов – от Франции, Юрий Манин – от Германии. 

Всего в академию Европы было избрано 86 российских ученых. Среди тех 71 человека, кто продолжает плодотворно работать, – литератор Мариэтта Чудакова (1991), физики Владимир Захаров (2011) и Алексей Хохлов (2000), биологи Георгий Георгиев (1989), Александр Спирин (1990) и Евгений Свердлов (2004), астрофизик Рашид Сюняев (1990), экономист Виктор Полтерович (1992), химик Александр Кабанов (2013), лингвист Андрей Кибрик (2013), иммунолог Сергей Недоспасов (2010). 

15 россиян, членов Академии, уже умерли. Среди ушедших – социолог Татьяна Заславская, физики Виталий Гинзбург, Дмитрий Дьяконов и Сергей Капица, славист Владимир Торопов, историк Александр Фурсенко, математик Роланд Добрушин.

В 2015 году в Академию от России был избран только А.М. Вершик. Статистика на сайте  Academia Europaea показывает, что в этом нет ничего удивительного. Так, в 2014 году было избрано 7 россиян, в 2013 – 2 (Кабанов и Кибрик), в 2012 – 6, в 2011 – 7, в 2010 – 2 (Гельфанд и Недоспасов), в 2009 – 1 (София Георгиева), в 2007 – 2, в 2005, 2006 и 2008 годах – ни одного россиянина.  

Как отмечается в Википедиии на сайте организации, Европейская академия  — общественная неправительственная организация, призванная объединить ученых всех европейских стран. Она была создана в Кембридже в сентябре 1988 года в рамках концепции «Общеевропейского дома» и объединенной Европы. Академия включает секции по всем основным разделам естественных и гуманитарных наук и объединяет свыше 2000 ученых. 

Инициатором создания пан-европейской академии стало Королевское общество Великобритании. Выборы членов академии проводятся по отделениям после тщательной экспертизы научных заслуг номинантов, итоги выборов должны получить одобрение совета Академии. Среди членов – 52 лауреата Нобелевской премии, часть их которых была избрана в Европейскую академию еще до своего лауреатства. 

Мы публикуем стенограмму и видеозапись лекции, с которой выступил кандидат экономических наук, доцент факультета экономических наук НИУ-ВШЭ, экономист и политолог Алексей Владимирович Захаров. Лекция состоялась 14 мая 2015 года в рамках «Публичных лекций «Полит.ру» в Тургеневской библиотеке.

Текст лекции

 Сейчас я хочу немного рассказать о науке, которая называется «Теория игр». Это даже не совсем наука, это раздел прикладной математики, который используется при попытках осмыслить то, как люди и организации взаимодействуют друг с другом в окружающем нас мире. 

Вообще, Бог создал мир прекрасным, люди были добрые и между ними должна была быть любовь. Но Дьявол что-то такое подсыпал в этот котел, и появилась «дилемма заключенного». В хорошем мире такого быть, наверное, не должно. 

Поднимите руки те, кто раньше видел эту вещь? Примерно половина, процентов сорок. Смотрите, вот это – лицо Зла на Земле. Каждый из этих двух человек подозревается в совершении некоего серьезного преступления. Их поймали, Васю и Петю, и говорят, что они подозреваются в совершении ограбления, они могут либо сознаться, либо молчать. Их разводят в разные камеры, не дают общаться друг с другом, читают каждому краткий курс «Теории игр» и рисуют каждому вот такую таблицу и объясняют им расклад. 

Расклад такой: если оба промолчат, то каждому «впаяют» один год за какую-то мелочь типа хранения оружия. Если один сознается, а другой промолчит, то тот, кто промолчит, получит «по полной». А тот, кто сознается, сразу же выйдет  на свободу. Наконец, если оба сознаются, если оба друг друга «заложат», то каждый получит срок, если не десять лет, то, скажем, восемь. 

Здесь матрица 2х2, каждая клеточка соответствует какой-то паре действий. Первая цифра в этой клеточке – это выигрыш Пети. А вторая цифра – выигрыш Васи. То есть, это не игра с нулевой суммой, когда либо один у другого отбирает, либо наоборот. Например, здесь каждому лучше, чем здесь. 

Давайте посмотрим, что будет делать Петя. Если Вася молчит, то Пете надо сознаться, потому что 0 больше, чем -1. Если Вася сознается, то Пете тоже нужно сознаться, потому что -8 больше, чем -10. В результате Петя сознается, и Вася тоже сознается, потому что у него симметричная игра. Получается так, что они оба, хлопая глазами, окажутся здесь, вместо того, чтобы оказаться здесь (показывает на слайде). 

Итоговый результат для каждого будет строго хуже, чем он мог бы быть, если бы они имели возможность координировать свои действия. 

На самом деле, главная мораль, которую мы можем извлечь из этого дела, это то, что так устроено взаимодействие между людьми, организациями, государствами, что итоговый результат не устраивает никого. 

Если бы договорились, было бы лучше и тому, и другому. Ан нет. И примеров тут полно. Гонки вооружений, допинг в спорте. Некоторые виды профессионального спорта, как здесь – тут две команды велосипедистов, одна использовала допинг, другая – нет. Было бы лучше, если была честная борьба? Да, было бы лучше. Но проблема в том, что тут есть нескольку субъектов принятия решений. Из-за этого у нас возникают сложности. То же самое с гонкой вооружений. То же самое с рекламой. «Кока Кола» и «Пепси» – они пытаются друг с другом воевать. Могли бы не воевать? Могли. Но кто же им прикажет одновременно обоим не воевать… 

Проблема общественных ресурсов. В Мировом океане в международных водах можно ловить рыбу. И, в результате, сейчас количество рыбы в Мировом океане, по крайней мере, в Атлантике, по некоторым данным в два-три раза меньше, чем было 50 лет назад. Все люди съели. Почему? Потому что есть много разных организаций, государств, которые занимаются промыслом рыбы, им трудно договориться, чтобы этот промысел рыбы был ограничен. Если бы они сделали это все вместе, если бы в этой матрице выбирались не строки и столбцы, а выбирались клетки, тогда была бы другая история. 

Другой похожий пример – это «ценовой сговор». Представим себе, что у нас есть несколько стран-производителей нефти. ОПЕК, например. В какой-то момент, в 70-х годах несколько крупных нефтепроизводящих государств договорились ограничить выпуск своей продукции. А потом в какой-то момент всё так повернулось, что им перестало быть выгодно поддерживать этот договор. То есть, выгоды от нарушения договора стали настолько большими, что сначала Саудовская Аравия, а потом и остальные страны были вынуждены выйти из этого договора. 

В принципе, это можно объяснить как задачу для первого курса микроэкономики. У нас есть две фирмы, давайте, мы смоделируем ситуацию, где каждая фирма решает, сколько ей произвести. Цена на рынке зависит от того, сколько в сумме было произведено двумя фирмами, прибыль фирмы равняется выручка минус издержки. Из-за того, что цена определяется как производство первой фирмы, так и производство второй фирмы, эти две фирмы сидят «в одной лодке». Так же, как и Вася с Петей в первой задаче. Отличием может быть то, что решением задачи с фирмой, что ей делать, зависит от того, что делает другая фирма. 

Но здесь можно показать, что, например, если спрос на продукцию становится слишком «эластичным», а «эластичный спрос» – это, например, когда количество альтернативных источников нефти становится большим, тогда в этом случае может быть так, что им будет выгодно друг друга «кинуть». И в принципе теоретико-игровые модели позволяют такие ситуации моделировать, объяснять на пальцах – что делать дальше. 

А дальше мы можем либо говорить, делать какие-то качественные выводы, показывать причинно-следственную связь между эластичностью спроса и тем, насколько долго будет жить картель (договоренность между двумя фирмами), либо мы попытаемся сделать количественный  прогноз, что сложнее. Потому что нам придется рассматривать не фирму в вакууме, а попытаться математически описать ее прибыль, издержки, для чего нам надо знать, что сколько будет стоить в рублях и еще какие-то дополнительные обоснования. Это сложнее. 

И на самом деле чаще мы ограничиваемся качественным анализом. Здесь я написал отличительную особенность теории игр, что она рассматривает несколько субъектов принятия решений. Если субъект принятия решения один, то тут мы говорим об оптимизации, это другая тема.  

Теперь – какие выводы мы можем делать? Мы можем делать выводы нормативного характера – что произойдет, либо мы можем давать какие-то рекомендации, например государству. Либо – самое важное приложение теории игр – это, наверное, дизайн механизмов. 

Представим себе, что у нас есть государство, которое производит аукцион частот мобильной связи. В Европе в 2000-х прокатилась волна аукционов, когда продавались частоты для связи третьего поколения. И выигрыш, который получили государства от продажи этих частот, очень разный. Великобритания выручила в 20 раз больше на абонента, чем Швейцария. Почему? Потому, что правительство Великобритании наняло очень «продвинутых» экономистов, которые прописывали условия аукциона. 

А у правительства Швейцарии все лоты частот были проданы по резервной цене, т.е. правила аукциона были прописаны так, что фирмам очень легко было вступить в неявный сговор друг с другом. Дизайн механизмов – обратная задача. Это не когда мы говорим, как будут люди себя вести, или как фирмы будут себя вести в зависимости от того, в какой игре они находятся, а когда мы ставим цель и говорим, какой должна быть игра, для того, чтобы эта цель была достигнута. 

Применение теории игр – на ней строится вся экономическая наука. Политическая наука в значительной степени – тоже. Чем экономика отличается от политики? Экономика – купил колбасы или положил деньги в банк. А политика – это проголосовал или не проголосовал. Это тоже принятие решений, но это принятие других решений. Большое количество прикладных задач, военное дело. 

Представим себе – летит самолет, в него запустили ракету. У ракеты есть какой-то алгоритм преследования самолета. У летчиков есть инструкции, как от ракеты уворачиваться. Тоже получается игра. Вопрос: как оптимально настроить ракету, чтобы она сбивала самолет, если известны инструкции летчиков, и как летчикам оптимально уворачиваться от ракеты, зная алгоритм наведения ракеты. 

Как мы математически описываем игру? Игра – это совокупность следующих сущностей: во-первых, набор игроков. Во-вторых, для каждого игрока прописывается, какие действия он может совершать. Ну, например, как у Пети  и Васи: либо молчать, либо сдаться. Потом мы для каждого игрока прописываем функцию выигрыша, то есть, как выигрыш игроков зависит от принятых ими действий. И вот, если мы эти вещи опишем, то у нас есть игра. 

Что нам дальше нужно сделать? Нам нужно найти какие-то действия игроков, сделать прогноз – как игроки будут себя вести? И самым распространенным способом сделать такой прогноз является равновесие Нэша. Что это такое? Это когда ни одному из игроков не выгодно в одиночку отклониться от своего действия. Джон Нэш – один из основателей этой науки, как раз про него снят фильм с Расселом Кроу в главной роли. 

Почему в игре должно быть какое-то равновесие, почему мы считаем, что игроки играют именно в равновесные стратегии? Вопрос: а в какие еще они должны играть? Если игрок играет в неравновесную стратегию, это значит, что он знает, что делают другие и действует себе во вред. Если мы предполагаем, что такого не происходит, значит, наши действия являются равновесными. 

Смотрите: здесь представлен пример игры, в которой равновесий несколько. Представим себе, что нет мобильных телефонов, а два человека должны встретиться в городе. И есть два места – театр и метро. Если они встречаются в одном месте – встреча происходит, если в разных – встречи не происходит. То есть, у нас есть некая игра, в которой есть два равновесия. На вопрос: какое из двух равновесий будет выбрано? – само описание игры ответа не дает. 

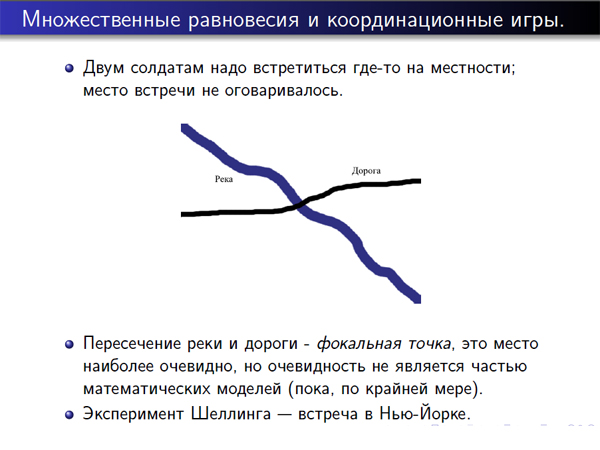
Вот еще пример такой игры: двух парашютистов высадили во вражеской местности, они потерялись друг с другом, а им нужно в одно место. Если они попадут в одно и то же место, то они выигрывают, если не попадут – то тогда их задание будет провалено. Вопрос: где они встретятся? Скорее всего, они встретятся там, где пересекаются река и дорога – на мосту. Почему на мосту? Потому что мост – это какое-то очевидное место. 

Мы можем математически описать игру. Если в игре есть несколько равновесий, то могут быть какие-то вещи, которые не входят в наше описание, которые могут влиять на то, какое именно равновесие будет более вероятным. Например, в 60-е годы в Нью-Йорке был такой эксперимент: двух человек в одно и то же время выпускали в разных концах города и говорили, что, если они в течение дня встретятся, то тогда получат по 100 долларов, а если не встретятся, то не получат. И, если люди были жителями Нью-Йорка, то большая часть людей встречалась – в Таймс-Сквер, под часами, в полдень. Если один или оба были не из Нью-Йорка, то тогда вероятность встреч была меньше. Если же они догадывались спросить, где встречаются нью-йоркцы, то тогда встречаться получалось. 

Теперь – за что Джону Нэшу дали Нобелевскую премию? Смотрите – в этой игре целых два равновесия. Это так называемая «конечная игра». Есть два игрока и у каждого игрока по две стратегии. Если у нас конечное число игроков и конечное число стратегий, то игра является конечной. Однако существуют игры, в которых равновесия нет. Например, игра «чет-нечет», упрощенный вариант «камень-ножницы-бумага». 

Играют два человека. Если сумма выкинутых пальцев четная, то один другому бьет «щелбан». А если не четная, то – наоборот. Понятно, что в таком понимании равновесия нет, потому что, если я знаю, что я получу «щелбан», то я выкину на один палец больше или на один палец меньше. 

Однако мы можем более широко посмотреть на определение стратегии, можем поговорить о так называемых «смешанных стратегиях». Представим себе, что я не просто решаю как выкинуть «чет или не чет», а решаю,  с какой вероятностью выкинуть «чет». Таким образом, моей стратегией является вероятность выкинуть «чет». Или в «камень-ножницы-бумага» – моей стратегией является вероятность выкинуть «камень», «ножницы» или «бумагу». 

Давайте попробуем сыграть: камень, ножницы, бумага! Раз, два, три – я выиграл. Так вот, Джон Нэш доказал, что, если мы будем рассматривать смешанные стратегии, то равновесие в конечной игре всегда существует. Это один из нескольких его результатов, за который ему дали премию. И второй важный момент, который можно извлечь из этой истории, что очень важную роль играют конвенции. Предположим, что они встречаются у метро, значит, они в следующий раз они встретятся у метро. 

Это так же, как в одном учебнике описан пример: в центре Нью-Йорка люди идут всегда по правой стороне тротуара на работу. Так принято. Если вы будете идти по левой стороне тротуара, навстречу толпе, то вас затопчут. На самом деле, если все вдруг решат, что надо идти по левой стороне, то никакой разницы не было бы. Однако так исторически сложилось – по правой, что мы и наблюдаем. 

Очень много из того, что мы наблюдаем, могла бы быть совершенно другой, если бы вдруг все скоординировались и делали по-другому. Вот еще один пример. У нас есть несколько студентов, которые пытаются написать экзамен, и каждый имеет возможность списать. Если он списывает, он получает выигрыш, равный единице, если не списывает – получает выигрыш, равный нолю. Плюс к этому – всех списывающих студентов наказывают. Но административный ресурс у преподавателя ограничен, он не может взять и поставить двойки всей группе, даже если и хочется. 

Предположим, что объем наказания составляет С: чаша гнева емкостью С выливается на голову всех списавших. И в этой задаче может быть несколько равновесий: если С меньше единицы, то все всегда списывают, если С больше n, то никто никогда не списывает, если С между единицей и n, то существует два равновесия: в первом равновесии все списывают, во втором – никто не списывает. 

Борис Долгин: Что считается равновесием? 

Алексей Захаров:Равновесие – это такая конфигурация действий, что ни один из студентов в одностороннем порядке не захочет поменять свое действие. Равновесие – это такой профиль действий. Вот, например, Маша, Вася и Петя списывают, Оля, Катя и Миша – не списывают. Это пример профиля действий. 

Равновесие – это какой-то один профиль действий, такой, что ни один из студентов не захочет поменять свое действие, не получит выгоду, если он отклонится от своего действия. 

Можно привести другие примеры – парковка на улице. Если все игнорируют знак «Остановка запрещена», то, если количество эвакуаторов в городе не слишком большое, то возможны два устойчивых состояния: когда все знают, что их машины эвакуируют, и никто не паркуется, а кто паркуется – будет белой вороной, которую эвакуируют. Либо может быть, что все на всё наплевали, эвакуаторов не хватает, кого-то эвакуируют, но вероятность эвакуации слишком мала, чтобы остановить нарушителей. Понятно, что, если эвакуаторов слишком много, то тогда одно из этих равновесий схлопывается. 

Еще один пример позиционной игры: массовые протесты. Эту историю в своем блоге рассказывал один российский оппозиционный политик, которому пожаловался некто из Туниса, который сказал: «Мы в Тунисе такие все неактивные, это – страшная дыра, люди смирились и приняли такую судьбу. Наш диктатор будет вечно, а потом – следующий». Вот нечто такое пессимистическое он сказал, а через две недели в Тунисе произошла революция. На «ровном месте». 

Давайте, попробуем построить такую модель. Представим себе, что у нас есть k человек, и каждый из них решает, участвовать или не участвовать ему в каком-то мероприятии. Это может быть любое (мероприятие): выйти на улицу в акции, либо купить швейцарский франк, продав доллары. На самом деле, многие модели описание массовых акции имеют очень много общего с моделью фондового рынка. У нас тоже много участников, каждый из которых предпринимает какие-то действия, а выигрыш может зависеть от числа участников. 

И давайте предположим, что у нас выигрыш человека зависит от числа людей, принявших участие в этой акции. Но при этом люди разные – кто-то может выйти один, ему все равно, сколько человек встанет рядом с ним. Некоторые делают по-другому: пока весь город на улицы не выйдет, он будет сидеть дома. 

Предположим, что у нас есть пять человек. Для одного человека критическая величина равна единице, для двух других она равна трем, для четвертого и пятого она равна пяти. У нас есть три равновесия. В первом равновесии у нас одиночка выходит на улицу. Как в 1968 году, после событий в Чехословакии, всего несколько человек вышли с протестом на Красную площадь. Во втором равновесии протестовать выходят трое, в третьем равновесии выходят пятеро. 

Может происходить переход между этими равновесными состояниями, и тогда в Тунисе, где ничего отродясь не было, вдруг что-то начинается. Это – первый вывод. Второй вывод такой, что давайте, рассмотрим два города. В одном живут пять человек, со следующими критическими величинами: для двух человек критическая величина равна трем, а для трех других она равна 20. Во втором городе живут 10 человек, и это – город А, умноженный на два. В нем четверо имеют пороговую величину три, и шестеро имеют пороговую величину 20. В городе А есть одно равновесие, когда никто ничего не делает. В городе В появляется второе равновесие, при котором первые четверо принимают участие в этом действии, потому что четыре больше трех. Вроде бы, у нас те же люди, с теми же предпочтениями, просто их стало больше. 

Уточняющий вопрос:Скажите, а k_i– каков его физический смысл? Это мотивация конкретного участника? 

Алексей Захаров: k_i– это сколько нужно единомышленников, которые стояли бы рядом с вами для того, чтобы вы согласились что-то сделать.

То есть, если возвращаться к примеру гражданских действий, они часто происходят в больших городах, когда много людей рядом, и это не страшно. Поэтому бывали примеры, когда тоталитарные государства переносили столицы. Последние из таких разговоров идут сейчас в Египте – о том, чтобы столицу сделать в новом месте, видимо, власти решают, как себя обезопасить. А если город маленький, то там, конечно, протестовать сложнее. 

Следующий момент, о котором я хотел бы поговорить – динамические взаимодействия. Здесь мы рассмотрели несколько примеров, и в каждом из этих примеров люди принимали решения одновременно. Как, когда мы играем в «камень-ножницы-бумага»: я не знаю, что он выкинет, он не знает, что я выкину. 

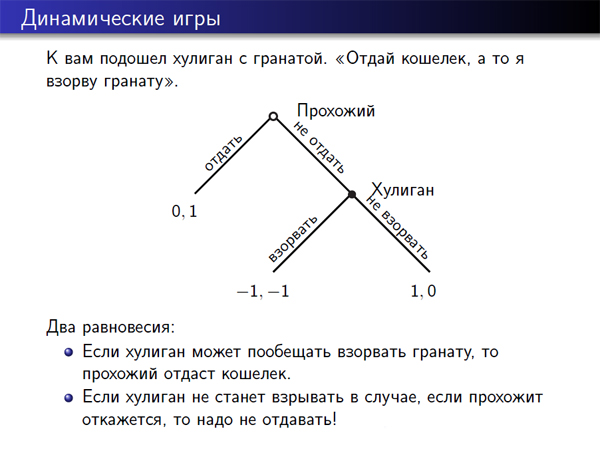
А теперь рассмотрим ситуацию: вы вышли погулять, ветерок колышет вам волосы, и вдруг к вам подходит парень с «приветом» в глазах и с гранатой и говорит: «Отдай кошелек, а то я взорву гранату». У вас есть варианты: отдать – не отдать, у него есть варианты взорвать – не взорвать. Но здесь есть некоторая очередность: сначала принимаете решение вы, потом принимает решение он. После того, как вы приняли свое решение, вы его уже не можете переиграть, потому что, если он вынимает чеку из гранаты, то игра заканчивается. 

Вопрос: как развернется эта ситуация? И ответ здесь зависит от того, насколько хулиган принципиален. Насколько он будет готов претворить в жизнь свою угрозу. Мы предполагаем, что предпочтения такие: лучше всего – быть живым и иметь кошелек; следующий вариант – быть живым без кошелька и самый плохой вариант – когда хулиган взрывает гранату. 

Если мы предполагаем, что хулиган – человек принципиальный, и, если сказал, то он сделает,  то, конечно, лучше отдать кошелек, потому что ноль больше, чем -1. Однако, если мы предполагаем, что у хулигана есть «тормоза», то есть, у него есть выбор – взорвать гранату или остаться без кошелька, если вы не отдаете его, то в данном случае он не взорвет гранату, а вы, зная это, не отдадите ему кошелек. 

То есть, мы, глядя на эту игру, можем извлечь такой урок: в любой ситуации, когда есть динамическое взаимодействие, очень важную роль играет возможность сторон сдерживать данные обещания. Например, почему очень важно иметь независимый Центральный банк? Хотелось бы всегда иметь возможность позвонить директору Центрального банка и сказать: сейчас нужно немного простимулировать экономику, давайте, сделаем что-нибудь.

Проблема в том, что такому Центральному банку никто не будет верить. Любой гражданин, когда будет решать, в какой валюте он будет хранить свои сбережения, будет понимать, что Центральный банк подвержен конъюнктурным запросам. 

Опять же – войны. Определенный процент войн начинается потому, что одна сторона не верит в возможность того, что вторая сторона не нападет первой, поэтому и нападает первой. Можно построить определенный аргумент, что  довольно часто демократизация происходит сверху. Элиты решают, что нужно ослабить политический контроль.  

Как можно объяснить такие решения? Это происходило в Латинской Америке, в Восточной Европе в последние 30 лет. Как можно объяснить добровольный отказ от власти? Можно объяснить тем, что элиты понимают, что, если не откажутся от власти, они не смогут сдержать обещания определенным образом перераспределять доходы между гражданами. И, если граждане не верят их обещаниям, то их могут свергнуть, уже более насильственным путем. 

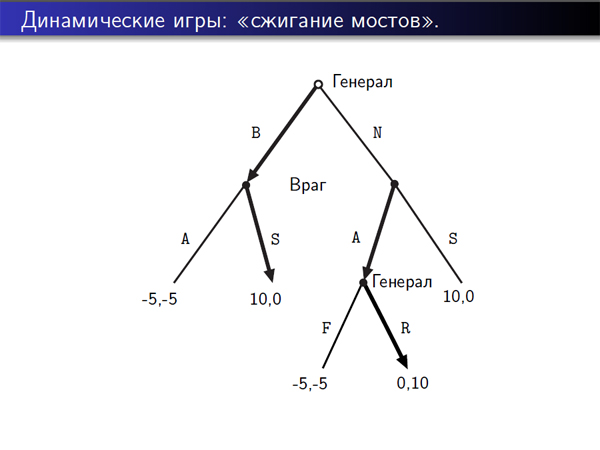
Здесь представлен пример игры, когда принимается некоторое сознательное действие, чтобы можно было сдерживать обещание: смотрите, мы предполагаем, что у нас два игрока – генерал, который командует армией, и враг. Генерал защищает город, который отделен от вражеской территории мостом. И сначала генерал решает, сжечь мост или не сжечь, а потом враг решает – напасть или не напасть. В том случае, если мост не сожжен, то генерал решает, бежать или не бежать. И в принципе, можно так подобрать выигрыши, что рациональным действием для генерала будет сжечь мост, чтобы не было возможности бежать, и враг, зная, что у генерала нет возможности бежать, не напал. 

Давайте, поговорим о том, какие пределы применения есть у теории игр? В каких случаях уместно, а в каких случаях – не уместно ее использование, чтобы моделировать человеческое поведение? 

Я был в третьем классе, когда понял, что в «крестики-нолики» всегда можно добиться ничьей. Эта игра была решена. Шашки. Английские шашки – это те, где можно бить только вперед, и дамки ходят только на одну клеточку. Английские шашки тоже недавно были решены. Было найдено так называемое «слабое решение», когда мы, начав игру, оптимальным образом реагируем на ходы другого игрока. «Сильное решение» – это когда мы можем подойти к доске в любой момент, сменить игрока и дальше оптимальным образом игру продолжить. «Слабое решение» было найдено – было проанализировано примерно 5х10²⁰позиций, (когда результатом) была ничья. 

Шахматы. Тоже есть какое-то решение. Мы его не знаем, но оно есть.  Я не знаю, сколько времени должно пройти, потому что там примерно 10⁴⁰позиций в шахматах, но со временем игры в шахматах будут проходить так: для тех, кому понятно, кто какими фигурами играет, гроссмейстеры будут подходить, пожимать руки, и игра будет заканчиваться. 

Но теория игр довольно хорошо моделирует игру «Крестики-нолики», довольно плохо моделирует исход шахмат, шашек, хотя в последнее время, как я слышал, довольно большой процент игр «на высоком уровне» заканчивались «ничьей», и теория игр ничего не говорит нам о том, как люди должны играть в шахматы. 

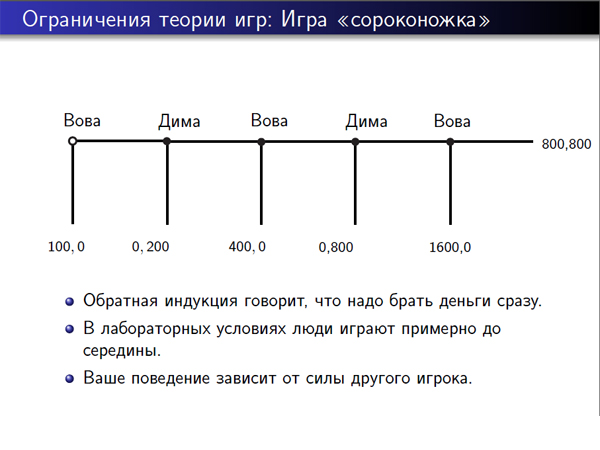
Вот еще пример игры – игра «Сороконожка». Предположим, что есть два игрока – Вова и Дима. Вове дали 100 рублей, он может их либо забрать, либо передать Диме. Эта сумма удваивается, и у Димы становится 200 рублей. Он может их либо забрать, либо передать обратно Вове, и у того становится 400. И так далее. И в самом конце Вова может либо забрать 1600, либо деньги делятся поровну. 

В этой игре обратная индукция – то есть, надо начать решать с конца: как здесь поступит Вова, а как здесь поступит Дима, если Вова поступит так, как надо, и так далее. Обратная индукция говорит, что деньги нужно брать сразу. Однако в лабораторных условиях, если мы сделаем компьютерный интерфейс, через который люди будут играть в эту игру, то люди примерно посередине будут брать деньги. Потому что я не рассчитываю, что я играю с гроссмейстером по шахматам в эту игру, наверное, где-то там человек ошибется и я, может быть, где-то передам ему ход в надежде на то, что смогу «срубить» 400, а не 200. 

Кстати, поведение игроков такой игры зависит от сил другого игрока. Такие эксперименты проводились – если я знаю, что со мной играет шахматист, то я заберу деньги раньше, чем тогда, когда я знаю, что со мной играет обычный человек, не привыкший просчитывать свои ходы вперед. Кстати, если играют два гроссмейстера, то они берут деньги сразу. 

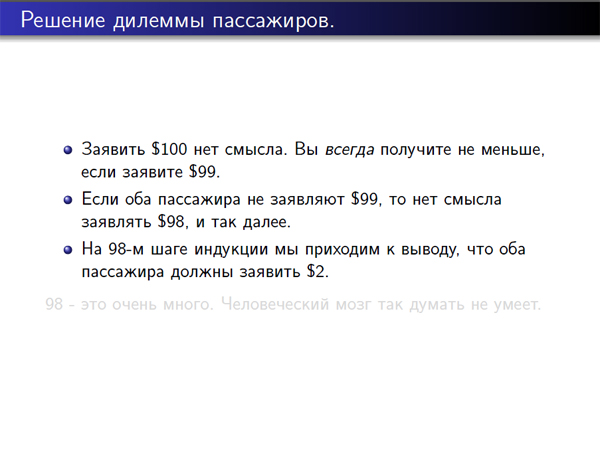
Еще пример. Предположим, у нас два пассажира следуют одним рейсом. У них пропали чемоданы. Авиакомпания предлагает им следующую схему компенсации: каждый пассажир называет сумму от 2 до 100 долларов, если оба сообщат одну и ту же сумму, то каждый получит эту сумму в качестве компенсации. Если один сообщает сумму меньшую, чем другой, то каждый пассажир получит компенсацию, равную меньшей из заявленных сумм. При этом тот, кто заявил меньшую сумму, получит дополнительно два доллара, а тот, кто заявил большую – дополнительно потеряет два доллара. 

Каков прогноз в этой игре? Смотрите. Большинство людей говорят, наверное, о сотне. Однако всё не так. Заявить 100 долларов не имеет смысла, потому что мы получим сумму не меньшую, если заявим 99. Это легко показать, что, заявляя 100, вы получаете строго больше, заявляя 99 – вы получаете 2 доллара «сверху», 101. Если другой заявляет меньшую сумму, чем 99, то вам все равно – что 100, что 99. Но если оба пассажира знают, что никто не будет заявлять 99, то также нет смысла заявлять 98 и так далее, и в итоге каждый получает два доллара. Но для того, чтобы получить эту сумму – два доллара – надо этот аргумент повторить 98 раз подряд. 

Человеческий мозг не умеет просчитывать на 98 ходов просчитывать вперед. Поэтому в экспериментальных условиях люди в эту игру играют, называя суммы, близкие к 100 долларам. Хотя единственное равновесие Нэша – это когда каждый человек называет по два доллара. 

Сейчас я хочу рассказать вам пример, когда в реальной ситуации человек использовал теоретико-игровое мышление для того, чтобы принять правильное решение. Это было шоу на американском канале, когда «племя» высадилось на необитаемый остров, сезон 2000-го года. В последний день осталось три участника. И каждому участнику предстоит испытание. Далее совет племени – эти оставшиеся трое – решают, кого изгнать из племени. То есть, фактически, решает тот участник, победивший в испытании, потому что по правилам игры после победы в испытании его не могут изгнать. 

Наконец, когда остаются двое, то победитель определяется из числа оставшихся двух голосованием недавно выбывших участников. Такое вот «голосование симпатий». И у них осталось трое: Руди – пожилой человек, в плохой физической форме, но при этом – добряк, который всегда разруливал сложные вопросы с людьми, очень популярный, но испытание он почти наверняка проиграет. Келли – молодая женщина в хорошей физической форме, Рич – молодой мужик тоже в хорошей форме и при этом он на протяжении всего времени пребывания на острове был в хороших отношениях с Руди. 

Дальше начинается испытание: каждый из них забирается на столб, стоит на одной ноге, при этом одной рукой можно опираться на другой столб, но все равно это неудобно. Солнце, тропический остров. Испытание. Руди тоже забирается на столб, хотя понимает, что проиграет. Проходит 10 минут и тут Рич спрыгивает. Один из участников сдается и отказывается от дальнейшей конкуренции.

Почему он это сделал? Можно попытаться построить «дерево игры» для Рича. У него есть выбор: сдаться или не сдаваться. Он не изучал теорию игр, но эту логику он изложил в интервью, после того как в итоге стал победителем игры. 

Он просчитал так: если он сдается, то тогда природа, Бог или случай решают, кто из двух оставшихся игроков будет победителем испытания. После чего оставшийся игрок решает, кого из двух других, не победивших в испытании, изгнать с острова, а после этого зрители решают, кого из двух оставшихся назвать победителем. И Мич подумал так: если он выиграет испытание, то он окажется в очень неприятной ситуации. Потому что, если он изгонит с острова Келли, то все симпатии достанутся Руди, если он изгонит с острова Руди, то люди ему это припомнят, и победителем будет объявлена Келли. 

И, когда он пришел к этой мысли, он спрыгнул вниз. Келли до этого не додумалась, она оказалась победителем этого испытания, была вынуждена выбрать, кого изгнать с острова – Рича или Руди, она изгнала Руди, и зрители проголосовали за Рича. Рич повел себя так, как будто изучал теорию игр. 

Наверное, на этом месте я закончу. 

Обсуждение лекции

Борис Долгин:Итак, мы услышали, как устроена теория игр и некоторые примеры того, как она рассматривает вопросы. А можно какой-нибудь пример того, как ее используют? Был упомянут пример про распределение частот сотовой связи, но мне кажется, что об этом можно рассказать поподробнее. 

Алексей Захаров:  Как я понимаю, вопрос о том, как теория игр используется на в науке, а на практике? В экономической науке – это просто стандартный язык, на котором люди друг с другом общаются. 

Представьте, что мы хотим исследовать вопрос, как институты влияют на экономическое развитие,  или как защищенность прав собственности влияет на то, насколько быстро меняется власть. Если мы будем исследовать, не прибегая к математическому языку, мы сильно осложним себе жизнь. Если я начну делать доклад на эту тему, и у каждого человека будет отдельное от других мнение о том, что я имею в виду. Описание ситуации в теоретико-игровой задаче  этот вопрос снимает. 

Теперь про сельское хозяйство. Здесь два главных момента. Первый – проведение аукционов, нужно прописать правила проведения. Например, у меня есть картина, я хочу ее продать. Как мне сделать так, чтобы продать ее подороже? Что нужно написать, как должны подниматься заявки и так далее, и как максимально возможным образом снизить сговор – при госзакупках? Второй момент – политика, Центральный банк, это макроэкономика. 

Как выглядит современная макроэкономическая модель? Она строится, исходя из предположений о том, как ведут  себя домохозяйства и отдельные люди. Центральный банк напечатал деньги – какой толк от этого будет? Будет ли это стимулировать экономику или это приведет к инфляции? Это главный вопрос, ответа на него нет. 

Наши знания о том, как экономика реагирует на такие шоки, улучшаются, но улучшаются посредством того, что каждый раз разрабатываются какие-то новые модели, в которых, как мы предполагаем, есть большое количество домохозяйств, каждое из которых принимает оптимальное решение  с точки зрения сделать себе лучше. Это – теория игр. 

Борис Долгин: Спасибо. Мне было все равно, народное это хозяйство или наука, важно было понять – к каким небанальным результатам приводит переход на этот язык. Вопросы? 

Вопрос: А какие ограничения существуют в применении теории игр? Именно в общественных науках? 

Алексей Захаров: Про одно ограничение я говорил – игры лучше моделируют ситуации, в которых людям не приходится думать на много шагов вперед. Это с одной стороны. С другой стороны – есть некоторое количество задач, которые теория игр пока не может «расколоть». Человек не думает, как машина, человек – сложный, есть большое количество поведенческих парадоксов, все они описаны. 

Давайте, я приведу вам в пример еще одну задачу, которая не поддается теории игр. Задача голосования. Почему люди голосуют? Предположим, у нас есть 100 человек, есть два кандидата. Один нравится 50 людям, другой кандидат нравится 50 другим. Каждый решает, голосовать или нет. Голосование сопряжено с издержками: я вышел на улицу, где может упасть на голову сосулька, я могу поскользнуться, я не посмотрю свой сериал – зачем мне голосовать, и так без меня все решат. 

Математически голосование оправданно тогда, когда достаточно велика вероятность того, что ваш голос будет решающим, что кроме вас голоса разложатся 50% на 50%. На выборах муниципального масштаба такие прецеденты в мировой истории были, но их можно пересчитать по пальцам двух рук. На национальных выборах такого нет и, наверное, быть не может. Ваш голос будет решающим, если будет миллион голосов на миллион, а вы будете два миллиона первым. Но люди, тем не менее, почему-то голосуют! 

При этом сравнительная статика такая же, как и предсказывает теория – чем больше электорат, тем ниже явка, но при этом она намного  выше, чем должна была бы быть, если бы люди были роботами. Так что этот вопрос затрагивает аспект человеческого поведения, который такая формулировка пока не очень может «расколоть». 

Реплика:Ваша последняя задача про Келли, Руди и Рича. Там Руди популярный, а Рич – это который сразу сдался. Но у Рича не было бы шансов, если бы Келли была умнее. Я так считаю. 

Алексей Захаров:Но вот оказалось, что она не была умнее, он был умнее. Ему повезло. 

Реплика (продолжение):Парадокс. Поэтому дело не в Ричи, а в Келли. 

Вопрос:Я с удовольствием прослушал пример про потерянный багаж, и это мне напомнило задачу о заключенных. Когда палач заходит в камеру и говорит заключенному, что его казнят на следующей неделе после полудня. Знакома вам такая? Палач говорит: «Вас казнят на следующей неделе после полудня, но не в воскресенье». Узник начинает думать: «Если не в воскресенье, значит, в субботу. Но я знаю, что это будет в субботу – значит, это будет в пятницу». И так, путем вычитания, он понимает, что его вообще не казнят. 

Реплика:Но по условиям он вообще не должен знать, когда его казнят! 

Алексей Захаров:Это не теоретико-игровая задача, это просто какая-то математическая задача. 

Реплика:Это демонстрация парадокса индуктивной логики? 

Борис Долгин:Правильно ли я понял: был вопрос об ограничениях в теории игр. Вы не видите впереди какого-то объединения теории игр и когнитивной психологии? 

Алексей Захаров:Давайте, я приведу пример. Когда мы говорим о выигрыше, мы можем иметь в виду всё, что угодно. Мы предполагаем, что у человека есть понимание, что этот исход лучше, а этот исход – хуже, что исходы человек как-то ранжирует. Но это не обязательно должен быть миноритарный выигрыш. 

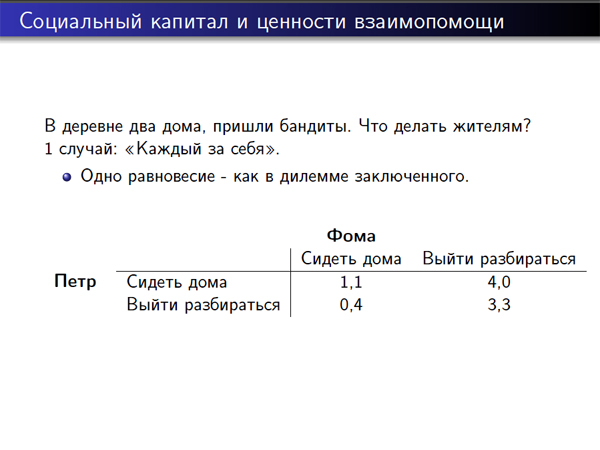
Представим себе, что в деревне – два дома, и в деревню пришли бандиты. И у каждого жителя есть два варианта: либо сидеть дома, либо выйти разбираться. Вот слайд: предположим, что выигрыши такие. Если они оба будут сидеть дома, то каждого ограбят, если она оба пойдут разбираться, то они бандитов победят, если один пойдет драться, то его убьют. А другого оставят в покое и даже не зайдут к нему домой. Что у нас здесь происходит? Оба сидят дома, и получает выигрыш один. 

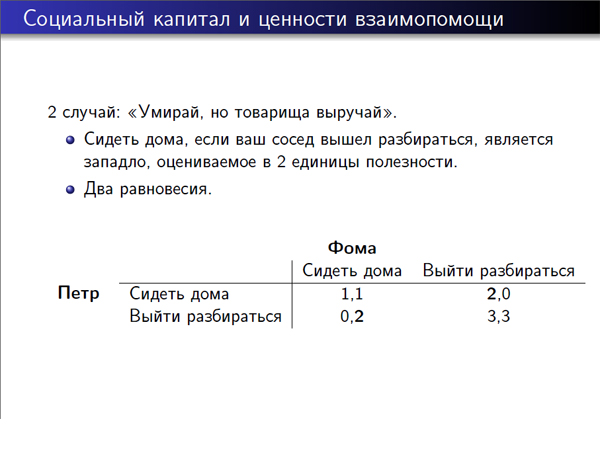
Вот второй слайд: предположим, что каждый был воспитан так, что должен выручить товарища, что сидеть дома, если сосед вышел разбираться, это «западло». И это оценивается в две единицы полезности. Тогда у нас получается такая матрица выигрышей, где жирным обозначается измененные значения. И здесь у нас получаются уже два равновесия, то есть, вариант «выходить разбираться» тоже является равновесием. 

Что такое «социальный капитал»? Это какой-то набор моделей поведения, которые позволяют людям лучше и легче взаимодействовать друг с другом и решать коллективные задачи. Вот пример того, как наличие социального капитала может быть препарировано в интересах игровой модели. Насчет именно когнитивной науки – знаете, пока рано говорить.

Борис Долгин:Хочу пояснить, почему я об этом спросил: теория игр стала в какой-то момент господствующей в теории принятия решений, в самом начале, затем возникли Сайман, потом – Тверский и Канеман, которые подошли к теории принятия решений уже с позиции когнитивной науки, но при этом никто теорию игр никуда не «задвигал». Отсюда и возникает вопрос: будет ли взаимодействие? 

Алексей Захаров: Это всё зависит от контекста. В каком-то случае контекст не очень подходит, в каком-то случае можно попытаться эти вещи как-то учитывать. Как здесь, например: в функции полезности мы можем учитывать какие-то психологические издержки. Либо наоборот. 

Борис Долгин:То есть, уходить от «человека экономического», оставаясь в рамках теории игр? 

Алексей Захаров:Да. Конечно. «Экономический человек» – понятие очень вульгарное. Мы просто предполагаем, что человек понимает, что для него лучше, а что – нет. 

Вопрос:Если я правильно понял, то при введении каких-то дополнительных условий в задачу всегда возникает определенная «равновесная точка»? При том – мы посмотрели другие примеры, где получается, что, когда люди договариваются, они всегда могут найти варианты, по которым их убыток, условно говоря, будет меньше. С точки зрения теории игр – все-таки, где полезность больше? Тогда, когда люди договариваются, или тогда, когда в игру вводят как можно больше разных дополнительных условий, чтобы «равновесная точка» становилась мощнее? 

Борис Долгин: Кажется, лучше начать отвечать с тезиса, который был вами неверно понят – что якобы появляется некая «точка равновесия» при внесении дополнительных условий. 

Алексей Захаров: Честно говоря, я не очень понял вопрос. 

Вопрос (продолжение):Ваш тезис: если есть конвенция, то «равновесная точка» есть всегда. Соответственно, мы видели, что тогда, когда идет теория игр, на примере двух заключенных: если они знают, как будет действовать другой, то они получают минимальный убыток. 

Борис Долгин:Что вы пытаетесь противопоставить ситуации коммуникации? 

Вопрос (продолжение):Еще раз вопрос: для того, чтобы люди получали наибольшую прибыль или наименьший убыток, что более выгодно? Научиться договариваться или вводить как можно больше дополнительных условий для того, чтобы равновесная точка была…

Борис Долгин:такого вообще не было, если я правильно понимаю. Договариваться, никакого «или» нет. 

Вопрос:Спасибо за лекцию. У меня вопрос такой: пытались ли на языке теории игр сформулировать ситуацию развязывания Второй Мировой войны? Была ли такая попытка предпринята кем-нибудь? Это первый вопрос. Второй: какую простенькую задачку вы сами лично сформулировали по поводу теории игр, и решили ли ее? Спасибо. 

Алексей Захаров:Про Вторую мировую: нет, мне не знакомо, чтобы она рассматривалась как игровой case-study. Но, в принципе, в других случаях другие конкретные ситуации могли рассматриваться. Например, во время Первой Мировой войны на Западном фронте война происходила, в основном, во время противостояния армий. С одной стороны были окопы, между ними была «ничья» земля, и с одной стороны – англичане, с другой стороны – немцы. Сражения были очень кровопролитными. Тогда наступательное оружие было слабее оборонительного, то есть, пулемет придумали, а танк – еще нет. 

Поэтому большую часть времени, когда не было сражений, просто сохранялся status quo. И, несмотря на то, что снайперы могли стрелять, люди были в пределах досягаемости оружейного выстрела, между двумя сторонами перестрелок практически не было. Почему перестрелок не было? Потому что люди реализовывали стратегию «око за око»: если стреляют в нас, мы немедленно открываем огонь на поражение. И в силу того, что друг другу противостояли одни и те же части в течение долгого времени, это было достаточно сдерживающим фактором для того, чтобы противники не открывали огонь на поражение. Хотя иногда огонь открывали для того, чтобы продемонстрировать, что могут попасть. 

Например, считалось круто пробить котелок у противоположной стороны, висящий над костром. Потом английское правительство решило, что это плохо и начало чаще менять войска и требовать регулярных разведывательных рейдов на вражескую территорию и предъявлять в качестве результатов либо собственные потери, либо пленных. И вот это требование разрушило хрупкое равновесие. Почему я говорю про теорию игр – потому что этот пример был приведен в известной книге Роберта Аксельрода «Стратегия конфликта». 

Теперь – о моем вкладе. Я могу рассказать о своей работе, которую я делал. «Компромисс между компетенцией и лояльностью для подчиненных в режиме диктатуры и за ее пределами». Диктатор решает, кто будет у него премьер-министром, а кто – министром обороны и так далее.  Очень часто намеренно на эти посты выбирают некомпетентных людей. 

Почему это происходит, почему лояльность ценится выше компетентности? Николай I, когда узнал про одного из своих приближенных, очень грубо проворовавшегося на фонде инвалидов, присвоив себе большую часть денег, в сердцах промолвил: «Рылеев и его сообщники этого бы со мной не сделали!» Он понимал, что берет на работу людей менее компетентных, чем декабристы, но при этом более верных. 

В принципе, можно построить игровую модель, которая будет объяснять, почему в некоторых случаях на работу берут более верных, нежели компетентных. Представьте себе, что меня взяли на работу, а моя работа – продлевать сроки пребывания у власти. Я могу поехать на Канары, или я могу остаться на своем посту и проявлять большее усердие, чтобы мой покровитель с большей радостью остался у власти. И плюс я могу еще делать другие вещи, в которых я более или менее компетентен. Иногда бывает такая логика: почему на работу берут некомпетентного человека – потому, что он больше никому не нужен, и он будет держаться за свое место. В принципе, это такой common sense, но можно построить игровую модель, которая будет объяснять это, и будет говорить – в каких случаях это скорее происходит, в каких – скорее не происходит. И это – одна из вещей, которая меня интересует. 

Борис Долгин:Могу подтвердить: известный специалист в области истории госучреждений и общественных организаций покойный Александр Давидович Степанский рассказывал как о некотором базовом принципе, что наименее «качественный» сотрудник органов управления обычно выдавливался из учреждения на повышение. Речь шла о дореволюционной России XIX - начала XX века. 

Вопрос: Я был на лекции вашего коллеги Александра Елисеева. Он говорил о подходе к решению комплексных проблем. Комплексная проблема – это такая проблема, о которой мы зачастую не знаем, ни в чем сама проблема, ни каков ее исход. В этой связи у меня два вопроса: можно ли использовать теорию игр для определения, что является выигрышем. То есть, у нас есть несколько участников, мы начинаем игру, мы чувствуем, что у нас есть какая-то проблема, мы начинаем пытаться ее решать, но не знаем, в чем состоит проблема и каков будет наш выигрыш. Вот к таким ситуациям формализм теории игр применим? 

Мы не можем формализовать наш выигрыш. То есть, мы хотим понять, для чего мы собрались, и какой опыт мы хотим получить, что хотим знать.. Это первый момент. И второй момент – допустим, есть какая-то проектная группа, они решают какую-то неструктурированную проблему, задачу. У них возникает в группе определенная динамика. Теория игр применима для  заключения процесса, который возникает внутри  проектных групп? 

Алексей Захаров:Начну с последнего вопроса. Ответ: да, применима. Потому что в любом коллективе есть проблема, что один человек делает, а другой «заказывает музыку», и он не может проследить, насколько усердно первый выполняет работу. Вторая проблема в том, что результат работы может быть плодом усилий нескольких человек. Например, если я точно знаю, сколько часов, минут и секунд мой подчиненный проводит на работе и насколько он выкладывается, то я могу оплату «привязать» к тому, как он работает. А если я не могу наблюдать, то мне приходится его компенсацию привязывать к результату. 

А если у нас результат – какая-то случайная величина, которая зависит от усилий, но не взаимооднозначно определяется усилиями, тогда у меня возникают проблемы, тогда, может быть, и не получится у меня выжать из него все соки, которые я бы хотел. Второй момент – у нас может быть несколько людей, которые вносят свой вклад в один и тот же результат. Вопрос, как мы будем компенсировать этих людей. В принципе, отношения того, как надо управлять коллективом – это очень широко исследуемая тема. А каким был ваш первый вопрос? 

Вопрос (продолжение): Он формально сводится общественной дилемме: пушки или масло? Такая избитая тема. Но бывает еще и комбинация. Может быть пушки и масло. А бывает, что ни пушки, ни масло, а что-то другое. Собирается коллектив и говорят: «На нас собираются напасть бандиты» (то есть, нужны пушки?). Но в то же время нужны рабочие руки, чтобы делать масло. Как сориентироваться – на что потратить свое время, чтобы, с учетом внешней обстановки… 

Борис Долгин: Переформулирую вопрос иначе. Можно ли методами теории игр государству разобраться с тем, как строить свою стратегию в бюджетных расходах? Исходя из реального набора угроз, задач, проблем, внутренних и внешних. 

Алексей Захаров:Если речь идет о внешней политике… 

Борис Долгин:О совокупности внешней и внутренней. Поскольку бюджет может тратиться на пушки, на масло и так далее. 

Алексей Захаров:Если вопрос – сколько тратится на пушки, ответ будет: все зависит от того, насколько серьезны угрозы. А серьезность угроз в том числе зависит от того, насколько другие страны могут друг с другом взаимодействовать. И здесь игровой анализ вполне уместен. 

Вопрос:Вы сказали, что есть ограничения по количеству решений, которые человек способен просчитывать. Вообще, насколько человеческий мозг способен просчитывать решения в игре? И что мешает сделать это с помощью компьютера? Либо на бумаге изобразить дерево игры и с помощью этого разобраться с игрой? 

Алексей Захаров:Ничего не мешает. Но люди редко все просчитывают при помощи компьютера. Когда я решаю – купить мне машину или стоит перевести деньги в рубли или доллары, или куда поехать отдыхать - я же не использую компьютер, я сам думаю. 

Вопрос (продолжение):Но бывают более сложные ситуации. 

Алексей Захаров:Мы сейчас говорим о «базовой» ситуации. Мы говорим о теоретико-игровой модели, макроэкономической. Субъектами принятия решений являются люди. Мы – матрица, решение этой проблемы. 

Борис Долгин:Нельзя ли создать индивидуальную систему поддержки принятия решений каждому человеку по всем поводам? Если я правильно понял вопрос. 

Алексей Захаров:Нет, нельзя. И, кроме того, до решения шахмат еще очень далеко. 

Вопрос:Уже давно в Интернете есть такая практика: люди участвуют в форумах, и на разных форумах совершенно разные характеры общения и комментов, сообщений. В одних случаях«троллят», в других – складывается нормальное общение. Причем, оно интересное, конструктивное для многих сторон. И по практике участия в подобных форумах, «комментах», оно складывается не сразу, но затем поддерживается в течение длительного времени. Даже тогда, когда субъекта обсуждения нет. Когда вопрос уже решен, люди продолжают взаимодействовать по сложившимся между ними отношениям. Можно ли и как это описать с помощью аппарата теории игр? 

Алексей Захаров:То есть, как формируются сообщества? Это очень интересная задача. Все-таки, наверное, мы здесь можем описать игровую задачу, однако концепцией решения у нас будет не равновесие Нэша, скорее всего, а просто какая-то перемоделированная динамическая система. Вот если мы хотим понять – как формируется сообщество в Фейсбуке. Наверное, мы поймем больше, если будем просто рассматривать как численные модели, как эволюционируют численные модели. 

Вопрос:Насколько я понимаю, теория игр оперирует людьми, которые думают над своей стратегией, стараются поступать рационально. Но, к сожалению, в жизни большинство людей действуют иррационально. Как вообще можно применять теорию игр в жизни, где большинство поступков – не рациональны? 

Алексей Захаров:Мы можем применять теорию, если мы предполагаем, что люди себя ведут так, как будто они ведут себя рационально. Вообще, что такое рациональность? Основное предположение, которое делается, это то, что у людей есть какой-то порядок предпочтения на множество исходов. Если вы считаете, что А лучше, чем В, если вы считаете, что В лучше, чем С, из этого следует то, что А лучше, чем С. 

Что такое рациональность? Дальше мы можем пытаться предполагать, что у людей есть какие-то случайные факторы, которые могут делать тот или иной выбор более или менее предпочтительный. Существует ровно один способ описать рациональное поведение, и миллион способов – описать не рациональное.  И можно различные аспекты нерациональности пытаться включить в рациональную модель. 

Вопрос:Алексей, у нас тут вопрос из Твиттера. Наши читатели интересуются – трудно ли построить карьеру политолога в современной России? К сожалению, вопрос не по теме. 

Алексей Захаров:Хороший вопрос. Что такое политолог? 

Борис Долгин:Видимо, в данном случае различают понятие «политолога» как специалиста в области политической науки и  политолога как популярного комментатора политических сюжетов. И, наверное, спрашивают о первом. 

Алексей Захаров:Конечно, наукой легче заниматься, если вы работаете где-нибудь в американском университете. Если вы живете в России, то найти хорошую работу сложнее. Поэтому ответ будет: «Нет, наверное, довольно сложно». 

Борис Долгин: Но является ли этот ответ специфическим для специалиста в области политической науки? 

Алексей Захаров:Не является. В общественных науках мало людей, которые этим занимаются. Наверное, это – одна из проблем… 

Вопрос: Добрый вечер, Алексей Владимирович. У меня вопрос, касающийся координации и механизмов. Когда мы спускаемся в московское метро, мы иногда видим таблички «Держитесь левой стороны». Во-первых, они не появляются, во-вторых, они появляются не всегда. Связано ли это с игрой на равновесие и как бы вы интерпретировали это решение? 

Алексей Захаров: Один мой коллега, который работает в одном из американских университетов, когда попал в московское метро, удивился, как здесь замечательно, как все с одной стороны стоят, с другой стороны – идут, потому что у них всё происходит вразнобой, и невозможно в метро по эскалатору пройти вверх. С одной стороны, у нас есть какая-то конвенция – люди привыкли с одной стороны стоять, с другой стороны – это дисциплинирует. 

Вопрос (продолжение):Речь не об эскалаторах, речь о переходах между станциями. 

Алексей Захаров:Переходы между станциями! Здесь то же. 

Вопрос (продолжение): Да! И в некоторых случаях написано «Держитесь левой стороны», а в некоторых – это не написано. Есть ли в этом задумка управленца, который это прописывал? 

Алексей Захаров:Я не знаю, если честно. Наверное, было бы очень интересно провести эксперимент. Можно в случайном месте в случайное время написать «Держитесь левой стороны», «Держитесь правой стороны», а потом посмотреть… 

Вопрос:Добрый вечер. У меня два вопроса, на которые можно ответить «Да» или «Нет», на ваше усмотрение. Вопрос первый: правда ли, что на математическом аппарате теории игр базируется доказательство теоремы Гёделя? 

Алексей Захаров:Я не могу ответить на этот вопрос. 

Вопрос:Вопрос второй. Скажите, существует ли обобщение теории игр не на целое число игроков, а на дробное число игроков? 

Алексей Захаров:Существует обобщение на континуум игроков. Полтора игрока невозможно. Возможно континуум и один игрок. Например: есть Центральный банк и куча мелких физ.лиц. 

Борис Долгин:Возвращаясь к первому вопросу, должен сказать, что у нас была лекция А.Б. Сосинского, посвященная теореме Гёделя, и он там не использовал аппарат теории игр. Но из этого не следует, что кто-то не может попытаться, хотя мне кажется это странным. 

Вопрос:Рассматривается теория игр. Но есть игрок, который правильно раскладывает ситуации, в которых игрок отказывается играть в эту игру. Возвращаясь к примеру на слайде, «авиакомпания и багаж». Игрок просчитывает все варианты. При потере багажа максимальный выигрыш составит, если стандартно рассуждать, 98 шагов – 2 доллара. Игрок говорит, что он не будет играть и подаст на компанию в суд. Такие ситуации рассматривались? 

Более общий вопрос: каким образом составить такие правила игры, которые максимизировали бы порядок (?) эффективности для остальных игроков? 

Алексей Захаров:Да, рассматривались. Это задача дизайна механизмов. Иногда это можно сделать, иногда нет. Если коротко. 

Борис Долгин:Но вообще, в каком-то смысле описанный случай с действием по отношению к авиакомпании не является выходом из игры. Он является одним из действий в рамках игры. 

Алексей Захаров:Да, правильно. На самом деле, если про первый вопрос, как я его понял: что мы можем просто моделировать выход из игры как одно из действий в игре. Давайте предположим, что стратегия такая: молчать, сдаться, застрелиться. У вас всегда есть шанс застрелиться. И дальше мы так же будем это анализировать. 

Вопрос (продолжение):Там выход из игры не рассматривается как стандартный? Как стандартная матрица? Нет такой третьей колонки «Выход из игры»? 

Алексей Захаров:Почему? Да, будет такая колонка «Выход из игры».

Вопрос:Вы давно занимаетесь теорией игр и, наверное, знаете все сообщество в Москве, в России, которое изучает и практикует теорию игр? Знаете ли вы доподлинно, какие-либо  органы власти, институты, которые регулярно, осознанно применяют теорию игр – Центральный банк, Генеральный штаб? Если этого нет, то должен быть спрос на такое. 

Алексей Захаров:Во-первых, я далеко не всех знаю. ЦБ – безусловно. Конечно, там работают люди, являющиеся академическими экономистами. Для академического экономиста это, безусловно, рабочий инструмент. Про Генштаб – не знаю, не скажу. Не знаком с ситуацией, вполне может быть. В силу их специфики они не обнародуют свои работы. МИД – то же самое, ответ – «Не знаю». 

Борис Долгин:Могу сказать, что в «позднесоветские» времена экспертиза какого-нибудь Института системных исследований использовалась различными государственными органами. И понятно, что специалисты оттуда, конечно, использовали теорию игр. Просто немного странный вопрос в том смысле, что это – не достижение прошлого года, которое специалист может знать или не знать. Это слишком глубоко вошло в специальность, в экспертизу и т.д. 

Вопрос:  Скажите, можно ли в игре учесть ситуацию, когда кто-то из участников заблуждается относительно того, в чем его выгода, и начинает действовать себе во вред? Не разрушит ли это все «равновесные точки»? 

Алексей Захаров:Ну, как он может действовать себе во вред? Обычно мы предполагаем, что, если человек решает делать что-то одно, а не что-то другое, то он по определению предпочитает делать то, что выбирает. Он сам решает, где ему вред, а где – польза. 

Вопрос (продолжение):То есть, мы считаем, что все участники игры по определению разумны? То есть, никто из них не заблуждается относительно того, что ему полезно? 

Алексей Захаров:Да, именно так. 

Борис Долгин:Если я правильно понимаю, то автор вопроса пытается различить субъективную и объективную пользу? 

Алексей Захаров:Смотрите, мы можем дальше еще какую-то стороннюю оценку его действиям приписывать. И смотреть, насколько с точки зрения сторонней оценки результат хороший – плохой. Но мы предполагаем, что у человека есть то, что он лучше других понимает, что ему надо. 

Вопрос:Скажите, существуют ли какие-то популярные программные пакеты, которые реализуют инструментарии теории игр? 

Алексей Захаров:Не знаю. Я даже не очень понимаю, зачем они могут быть нужны. Есть разные пакеты, которые помогают решать те или иные теоретические задачи, тот же «Матлаб», например. Наверное, есть какие-то модули в некоторых программах, которые помогают находить равновесие. 

Борис Долгин:Наверное, это может быть под какие-то конкретные случаи практического применения дизайна механизмов. 

Алексей Захаров:Я не думаю, что какие-то конкретные практические случаи. Все-таки на практике теория игр применяется все-таки как какой-то способ посмотреть на ситуацию «с другой стороны». На практике знание теории игр человеку, принимающему решения, просто помогает, расширяя кругозор. Все равно человек, принимающий решения, принимает их по совокупности теоретико-игровой ситуации, интуиции, прочих таких вещей. 

Вопрос: Я натыкался на эмуляцию «дилеммы заключенного», там можно было попробовать торговаться с Интернетом. У меня опять вопрос из Твиттера, опять офф-топик: с чем вы связываете сложность построения карьеры политолога в современной России? Как вы считаете, это потому, что в США построена либеральная демократия, а в России демократия гибридная? Или это связано с тем, что политическая наука – наука молодая? 

Алексей Захаров:Я готов на этот вопрос ответить кулуарно. Пусть человек мне напишет в Фейсбук, я отвечу. 

Борис Долгин:Попробуем обобщить вопрос: кажется ли вам более значимым фактором история политической науки в России или в какой-то другой стране, не важно. Или же сами особенности общей конфигурации режима, для которых какие-то социальные науки могут быть сложно представимыми, сложно одобряемыми и так далее? То есть, еще обобщая вопрос: здесь решающие внутри научные или вне научные факторы? 

Алексей Захаров:Решающие в чем?

Борис Долгин:Решающие в вопросе об эффективности построении карьеры внутри науки. 

Алексей Захаров: Если говорить про политическую науку, то даже на Западе она достаточно слабо соприкасается с практикой, хотя уже начинает соприкасаться сильнее. Политологов начинают привлекать в качестве консультантов для конкретных избирательных компаний, скажем так. Есть у них такая «опция». В принципе, вопрос «Готов ли я кого-то консультировать?» – может быть, и готов. Могут быть какие-то этические ограничения, которые не позволят мне с кем-то сотрудничать. Если мы говорим про спрос на это дело, какой-то уровень доверия… Нет, это очень сложный вопрос. 

Вопрос: Есть известные соревнования снарядов и брони. Растет уровень снаряда – растет уровень брони и так далее. В каком случае здесь достигается равновесие? Когда кто-то проигрывает? 

Алексей Захаров:Что такое здесь равновесие? Я не очень понял вопрос. 

Вопрос (продолжение):  Есть ли равновесие в такой соревнующейся военной технике? 

Алексей Захаров:Это равновесие в вопросе «сколько денег тратит каждая сторона на разработку снарядов и брони?». Его можно исследовать, делать какие-то выводы относительно того, что влияет на то, сколько тратит государство на разработку. 

Вопрос (продолжение): То есть, борьба не бесконечна? Равновесие, видимо, наступает тогда, когда кто-то проигрывает? 

Алексей Захаров:Не могу так утверждать. 

Вопрос: Учитывает ли теория игр, скажем, «боковые» результаты, когда игра с большим количеством итераций дает, например, какие-то эстетические картинка? Получаются какие-то совершенно неожиданные результаты, в которых имеется достаточно свой смысл, не связанный, может быть, с игрой? Как игра жизни, допустим, революция? 

Алексей Захаров:Еще раз, я не понял вопроса. 

Борис Долгин:Может быть, имеет смысл разбить вопрос на несколько частей? Первый вопрос: об играх с многочисленными итерациями? Этим теория игр вполне может заниматься. 

Алексей Захаров:Да. 

Борис Долгин:Второй вопрос: исходно в некоторых задачах всегда имеются в виду конкретные полезности. Может ли в задаче учитываться возможность появление новых, других полезностей? 

Алексей Захаров:У игроков? 

Борис Долгин:У игроков.

Алексей Захаров:Появление нового игрока – может ли быть такое? Может. 

Борис Долгин:В данном случае, видимо, речь шла о появлении, например, у игрока нового интереса. 

Алексей Захаров:Запросто. Можно предположить, что в следующий момент времени его выигрыш, если он пойдет направо, например, будет такая-то случайная величина с такими-то, такими-то значениями. Тогда мы говорим, что у него интерес может поменяться. 

Вопрос:Сколько слушаю про теорию игр, получается – может быть, я не прав совсем – что она описывает конечное состояние. То есть, мы сначала видим какой-то конечный результат, а потом описываем его модель и объясняем, что произошло. Но я не слышал, чтобы мы могли что-то спрогнозировать, причем, серьезно. Есть что-то, что теория игр именно прогнозирует, причем серьезно, доказывая полезность именно того или иного результата? Что, если мы вот так поступим, мы получим такой-то результат, это будет здорово. 

Борис Долгин:Я бы даже расширил: вариант «прогнозирует» и вариант «рекомендует». Тут явно были два оттенка сразу смешаны. 

Алексей Захаров:Можно ли прогнозировать, что что-то произойдет, если еще что-то сделать? Да, конечно, ради этого все и делается. Я не считаю правильным утверждение, что теоретико-игровая модель строится только тогда, когда наблюдается какой-то один результат. Военная наука с «обменными» ядерными ударами: смотрят, какие будут последствия, если кто-то случайно запустит – я сейчас фантазирую, но ведь наверняка такое делали – ракетой. И дальше аналитики пытаются просчитать, что произойдет. Но пока, слава Богу, никто ни одного запуска не совершил. 

Борис Долгин:То есть: а) прогнозируют; б) видимо, на этой основе рекомендуют? 

Алексей Захаров:И, видимо, на этой основе рекомендуют – что делать в том или ином случае.

Вопрос:Еще вопрос. Теория игр – это в большей степени дискретная вещь или больше логическая, аналитическая вещь? Чем больше оперируют в теории игр: конкретными цифрами, фактами, людьми, наборами людей – или это когнитивная модель? Когнитивная модель – она больше логическая. 

Алексей Захаров:Я понял. Ответ такой: значительно чаще теория оперирует со «сферическими конями в вакууме». Но иногда удается конкретную модель привязать к конкретным цифрам. Есть направление «Структурная эконометрика», мы пытаемся там анализировать выбор покупателей. Можно попытаться для покупателя построить его целевую функцию на основании того, какие товары он купил в супермаркете, в зависимости от цен. 

Я недавно работал в Турции, там экзамены в университет можно несколько раз подряд пытаться сдать. Были попытки оценить, как выглядит функция полезности для человека, который решает, стоит ли ему еще раз попробовать сдать экзамен, и сколько денег ему стоил тот или иной экзамен. То есть, когда можно, а можно не всегда, делаются попытки привязать модель к цифрам. 

Борис Долгин:Позволю себе завершающий вопрос: что еще читать кроме вашего учебника? Или – вместо этого учебника среди других, более-менее вводных книг в эту тематику? 

Алексей Захаров:Смотрите, моя книга – это университетский учебник. К сожалению, на русском языке мало, что есть. Литература на английском языке – тут, опять же, все зависит от уровня читателя. Например, хорошая книжка «Games of Strategy».

Можно выделить научно-популярные книги, но их проблема в том, что в какой-то момент для их понимания требуется математическая подготовка. Хотя бы на уровне знания мат.анализа и теории вероятностей. Поэтому в научно-популярных книгах какие-то вещи описаны хорошо, а о каких-то – информация не полная.

Есть специализированные книги, вроде моей, где базовые вещи и концепции объясняются. Есть книги более сложные, аспирантского уровня. Поэтому, лучше, наверное, прочесть хорошую научно-популярную книгу. «Games of Strategy» авторов Avinash K. Dixit, David H. Reiley Jr. 

Борис Долгин:Спасибо большое за лекцию!

8 ноября на церемонии в Исследовательском центре НАСА имени Эймса в Маунтин-Вью были названы обладателиежегодной премии за прорыв (Breakthrough Prize). Данная награда, учрежденная в 2012 году Марком Цукербергом, Юрием Мильнером, Сергеем Брином и Ма Юнеем, вручается в трех областях: науки о жизни, фундаментальная физика и математика. На этот раз лауреатами стали пять биологов, один математик и 1370 физиков.

По словам одного из основателей премии предпринимателя Юрия Мильнера, получившего образование по специальности «теоретическая физика», такое решение подчеркивает, что современная наука куда больше требует коллективных усилий, чем сто лет назад, становится более международной и вовлекает в исследование большое количество людей.

Как и Нобелевский комитет, комиссия по присуждению премий в этом году обратила внимание на доказательства существования нейтринных осцилляций (подробнее об этом можно прочитать в очерке «Нейтрино меняет маски»). Но если Нобелевскую премию по физике получили лишь руководители двух крупных исследовательских проектов, то Breakthrough Prize получат руководители и коллективы сразу пяти проектовпо исследованию нейтрино. Среди них Артур Макдоналди Нейтринная обсерватория в Садберри, Такааки Кадзита, Йоитиро Судзукии проект Super-Kamiokande, Коитиро Нисикаваи проекты KEK to Kamioka и Tokai to Kamioka, Ацуто Судзикии эксперимент KamLAND, Кам Бю Луки И Фанвани реакторный нейтринный эксперимент Daya Bay. Каждая из команд получает по 600 тысяч долларов. Руководители научных коллективов получат две трети премии, оставшаяся треть должна быть разделена среди участвовавших в проекте ученых.

Премию в области наук о жизни получили пятеро ученых. Неврологи Карл Дейссероти Эдвард Бойденбыли награждены за разработку оптогенетики – метода, позволяющего управлять электрической активностью нейронов при помощи света. Хелен Хоббсполучила премию за определение вариантов генома человека, влияющих на уровень холестерина. Джон Хардибыл награжден за нахождение мутаций в гене, кодирующем белок-предшественник амилоида, которые вызывают раннее начало болезни Альцгеймера. Наконец, эволюционный генетик Сванте Паабополучил премию за секвенирование древних геномов.

Кроме того, премию в области математики получил Ян Аголза доказательство трех гипотез о том, как трехмерные многообразия (многомерные эквиваленты двумерных поверхностей) могут становиться плоскими и трасформироваться. Полученные им результаты в будущем могут быть применены для понимания того, как искривляется пространственно-временной континуум. Ранее ученый получил за свои открытия премию Математического института Клэя.

В 1655 году английский математик Джон Валлис написал книгу, в которой он предложил формулудля числа Пи как бесконечного произведения дробных отношений. Спустя 360 лет два учёных из Рочестерского университета в Нью-Йорке – специалист по физике элементарных частиц Карл Хаген (Carl Hagen) и математик Тамар Фридман (Tamar Friedmann) – внезапно нашли эту же формулу в квантовых расчётах атома водорода. Статья американских учёных опубликована в Journal of Mathematical Physics.

«Мы не искали формулу Валлиса для числа Пи специально. Она сама упала нам в руки», – говорит Хаген. Он вёл у студентов курс квантовой механики и проходил с ними вариационный метод – технику с помощью которой можно приблизительно рассчитывать энергетических уровни в молекулах и других квантовых системах. Для примера Хаген взял атом водорода – один из немногих объектов, для которых положения энергетических уровней известны точно – и рассчитал эти значения с помощью вариационного метода.

В результате, он заметил интересную закономерность: погрешность для определения энергии основного состояния составила 15%, первого возбуждённого – 10%, а второго возбуждённого и следующих ещё меньше. Это необычная ситуация для вариационного метода: обычно погрешности в нём возрастают в обратном направлении – от самого низкого основного уровня и до высоких возбуждённых. Чтобы разобраться в этом Хаген нанял математика Тамара Фридмана.

Вскоре всё стало на свои места: учёные поняли, что большие погрешности для основного состояния объясняются очень маленьким размером атома водорода и как, как следствие, большими квантовыми неопределённостями в радиусе орбиты электрона. Но вместе с тем исследователи заметили и кое-то очень интересное: в формуле для рассчёта их убывающих погрешностей появился точной такой же ряд, как в формуле Валлиса.

«Это стало для меня полным сюрпризом, – рассказывает Фридманн. – Самое интересное, что здесь появляется такая изящная связь между физикой и математикой. По-моему это очень интересно, что математическая формула 17 века описывает физическую систему, которая была открыта тремястами годами позже».

Артур Шопенгауэр считал, что в основе человеческого юмора лежит непредсказуемость: нас веселит то, что обманывает ожидания. Спустя почти два века теорию знаменитого философа подтвердили эксперименты канадских и немецких учёных, которые показали, что самыми смешными людям кажутся слова с минимальной информационной энтропией или, проще говоря, слова, наименее вероятные. Исследование опубликовано в Journal of Memory and Language.

Термин информационной энтропии и формулу для ее расчёта впервые предложил американский математик, основатель теории информации Клод Шеннон. В его интерпретации энтропия была мерой неопределённости и непредсказуемости информации. Применительно к словам самые редкие и необычные из них обладают низкой энтропией и несут много информации – являются ключевыми для верного понимания текста какого-нибудь сообщения – а частые и привычные наоборот обладают высокой энтропией. Так, если выкинуть из предложения сверху слово «энтропия» или заменить его похожей по звучанию «энтальпией», то смысл сказанного будет полностью утрачен, а если вместо «обладают» случайно написать «обдают», то мы вполне сможем восстановить информацию, что называется, из контекста.

Чтобы проверить гипотезу о том, что самыми смешными нам кажутся слова с низкой энтропией, учёные провели несколько экспериментов. Сначала они давали испытуемым пары выдуманных слов и просили оценивать какое из них кажется более забавным. Потом же слова давались уже по одиночке и оценивать их предлагали не относительно друг друга, а по абсолютной шкале от 1 до 100: чем выше оценка, тем более смешным кажется слово.

В результате гипотеза подтвердилась: наиболее смешными людям казались самые необычные по звучанию слова. Внимательные экспериментаторы такими косвенным способом верно оценивали энтропию несуществующих слов более чем в 90 % случаев. Результаты исследования могут быть полезны в маркетинге: эту методику можно использовать, например, для проверки названий лекарств и отсева самых низкоэнтропийных из них, вызывающих, по мнению учёных, лишние смешные ассоциации.

Группа математиков из Университета Центрального Миссури (University of Central Missouri) обнаружиланеизвестное ранее простое число. Это самое большое на данный момент вычисленное людьми простое число. Для его полной записи в десятичной системе потребуется 22 338 618 цифр.

Математики охотились за простыми числами с тех пор, как около 500 лет до нашей эры на их существование обратили внимание древнегреческие ученые. Евклид (IV век до н. э.) доказало, что простых чисел бесконечно много, а Эратосфен Киренский (276 – 194 г. до н. э.) предложил алгоритм поиска простых чисел до определенного целого числа («решето Эратосфена»).

Новое простое число относится также к числам Мерсенна. Французский католический священник и монах Марен Мерсенн (1588 – 1648) изучал, в частности, числа, которые можно представить в виде 2ⁿ– 1, где n – натуральное число. Они обладают некоторыми интересными свойствами, например, если число Мерсенна – простое, то и показатель степени n для этого числа – тоже простое число. На этом свойстве основан тест Люка –Лемера для определения простоты очень больших чисел. Так как данный тест достаточно легко реализовать, самые большие из известных нам простых чисел оказываются числами Мерсенна.

Простое число, которое равно 2^74207281– 1, было обнаружено после 31 дня безостановочной работы компьютерной программы, созданной в рамках проекта GIMPS (Большой Интернет-поиск простых чисел Мерсенна). Программа использует распределенные вычисления на компьютерах пользователей интернета. Число было выявлено 17 сентября 2015 года, но из-за сбоя в системе обработки результатов его обнаружили в базе данных лишь 7 января. «Мы несколько смущены, что прошли мимо несколько месяцев назад, не заметив его», - признался руководитель проекта Кертис Купер.

Предыдущий рекорд самого большого известного людям простого числа продержался почти три года. Число 2^57885161 − 1 было вычислено 25 января 2013 года. Как и несколько предыдущих чисел-рекордсменов оно было получено благодаря проекту GIMPS.

Оксфордский физик Дэвид Граймс (David Grimes) создал математическую модель, которая предсказывает вероятность того, что тайный заговор будет раскрыт одним из участников или станет известным из-за случайных обстоятельств. Данные ученого позволяют считать, что, чем больше людей вовлечено в заговор, тем быстрее кто-то из них выдаст тайну. Поэтому наиболее известные конспирологические теории, вроде утверждений, что астронавты на самом деле не летали на Луну, не могут быть верными, иначе в течение нескольких лет кто-то из вовлеченных в заговор обязательно проболтался бы.

Граймс использовал данные о нескольких реальных тайных проектах, ставших известными из-за утечки информации, в том числе программу Агентства национальной безопасности США, раскрытую Эдвардом Сноуденом. Его вычисления показывают, что в наши дни, чтобы тайна оставалась тайной в течение пяти лет, число вовлеченных в нее людей не должно превышать 2521 человека. Хранить секрет десять лет смогут не более чем 1000 человек, а чтобы тайна продержалась сто лет, о ней должны знать не более 125 человек.

Оценивая число сотрудников НАСА, вовлеченных в лунную программу, в 411 тысяч человек, Граймс вычислил, что, если бы полет на Луну был мистификацией, она продержалась бы не дольше трех лет и восьми месяцев. Если бы крупные фармацевтические компании создали лекарство против рака и решили бы утаить его от общественности, это удавалось бы им три года и три месяца, после чего неминуемо произошла бы утечка этой информации.

Статья ученого опубликована в электронном научном журнале PLOS ONE.

28 января 2015 года в Независимом московском университете состоялась церемония вручения ведущему научному сотруднику Национального научного центра Франции, заведующему сектором ИППИ РАН, проректору Независимого Московского университета, доктору физ.-мат. наук Михаилу Анатольевичу Цфасману орденского знака рыцаря французского национального Ордена Академических пальмовых ветвей (chevalier dans l’Ordre national des Palmes Académiques). 

Торжественную речь о жизненном пути, достижениях своего коллеги в области математики и создания французско-российской научной лаборатории им. Понселе произнес вице-президент НМУ Алексей Брониславович Сосинский, носящий звание офицера этого ордена. Он сразу же предупредил, что М. А. Цфасману не придется как в средних веках вставать на одно колено перед королем, и король, увы, не положит ему меч на плечо. «Рыцарский орден будет просто прикреплен на лацкан пиджака», – сказал он. «А пиджака же тоже нет!», – захохотали присутствующие. 

«Орден академических пальм» был основан Наполеоном I и первоначально предназначался для того, чтобы награждать как учителей школ, так и вузовских преподавателей. Впоследствии его охват изменился, и орден принимает в свои ряды и деятелей культуры», – рассказал Алексей Брониславович. 

Видеозапись (неполная) церемонии:

Сосинский напомнил, что Михаил Анатольевич – москвич, происходящий из замечательной семьи врачей. «Мишин интеллект, его широкий культурный кругозор и острое ощущение потребности соблюдать нравственные ценности – всё это идет от родителей». Юноша сразу проявил тягу к науке. Он прекрасно учился в школе, очень рано проявил математический талант, учился во «Второй школе». Но для того, чтобы поступить на мехмат МГУ, где в те годы при поступлении отсеивали детей евреев и прочих неугодных советской власти, Цфасману пришлось стать олимпиадником, показать выдающиеся результаты на олимпиаде по математике в сборной СССР 1971 года. «По-французски есть хорошее выражение – его приняли de mauvaise grace (очень нехотя»)», – сказал Сосинский. 

Михаил учился на мехмате блестяще, под научным руководством Алексея Паршина и Игоря Шафаревича. «Миша выбрал самую старую и самую глубокую часть математики – теорию чисел и алгебраическую геометрию», – подчеркнул Алексей Брониславович. Антисемитский душок на мехмате МГУ не исчез и, несмотря на красный диплом, Цфасмана не допустили до экзаменов в аспирантуру, ему также «помогли» устроиться в третьеразрядный институт. В течение трех лет, положенных для отработки после вуза, Михаил продолжил заниматься математикой, в том числе в рамках семинара Юрия Ивановича Манина. 

«Через три года Юрию Ивановичу и другим коллегам удалось добиться, чтобы Цфасмана приняли в аспирантуру мехмата МГУ». В 1983 году Цфасман стал кандидатом физико-математических наук. До 1989 года нормальной работы найти не удавалось, но именно в этот период, в свободное время, Михаил совместно с Сергеем Влэдуцем (S.G. Vlădut) написал книгу «Algebraic-Geometric Codes». Книга была опубликована в изд-ве Kluwer Acad. Publ. в 1991 году и стала классической. 

После перестройки жизнь математика кардинально изменилась. Цфасман начал работать в ИППИ АН СССР и стал выездным. Первая поездка была судьбоносной – во Францию. В 1991 году он получает позицию директора по исследованиям CNRS. Желание как российских, так и французских ученых восстановить утерянные научные связи способствовало возникновению лаборатории Понселе (Poncelet), в которую Михаил Анатольевич вложил немало сил и времени. 

В заключение своей речи Алексей Сосинский в присутствии представителя посольства Франции вручил Орден и диплом академических ветвей новоиспеченному рыцарю.

Затем Михаил выступил с ответной речью, в которой отметил, что «ученый работает не для того, чтобы получать ордена, но признание всегда приятно». Он был очень рад, что орден ему вручили в стенах Независимого московского университета, являющегося «символом свободы и мудрости как в математике, так и для культуры вообще». 

«Лабораторию я создавал не в одиночестве, а вашими трудами», – сказал он собравшимся коллегам. Он подчеркнул особую роль Франции в его судьбе. «Первыми учеными, приехавшими в СССР повидать лично меня, были французы. Когда, к нашему всеобщему удовольствию, большевизм в стране рухнул, то именно французы пригласили меня за границу. Именно они уговорили меня начать с ними активно сотрудничать и предложили место в CNRS. Если бы не это, то совершенно естественным путем я оказался бы в США, но французы успели раньше». 

«Сегодня, когда мы смотрим на то, как развивается организация науки во Франции, то периодически мы видим, что то, что делает французское правительство – очень плохо для науки. Когда мы смотрим на то, что делают российские власти, то нам зачастую кажется, что они пытаются эту науку извести под корень. Хотя надеюсь, что они это делают совершенно естественным путем, не имея злых намерений. Однако наука продолжает существовать благодаря тем, кто понимает, что наука может существовать только на международном уровне, что она может существовать только исключительно усилиями ученых и, на самом деле, только вы не даете науке погибнуть. Да здравствует культура и мудрость, образование и наука! Да здравствует математика!». 

В церемонии приняли участие президент НМУ Юлий Ильяшенко; ректор Сколтеха, академик РАН Александр Кулешов; лауреат премии Филдса Станислав Смирнов; проректор МГУ, председатель Совета по науке при МОН Алексей Хохлов; президент Московского математического общества, академик РАН Виктор Васильев; новый глава лаборатории им. Понселе Сергей Нечаев и другие математики. Стоит отметить, что помимо Алексея Сосинского, Юлий Ильяшенко и Александр Кулешов – также являются кавалерами Ордена Академических пальмовых ветвей. 

Станислав Смирнов, Александр Кулешов и Алексей Хохлов

Алексей Ремович Хохлов, знающий Цфасмана с детства, обратился к рыцарю с речью. «Где-то с 1957 года мы жили в одном доме и ходили в одну прогулочную группу. Мы уже тогда обсуждали математические проблемы. Еще до школы мы обсуждали, какое самое большое число и, в конце концов, сошлись на том, что это, скорее всего, «бессчетное количество». А что? Вполне разумная гипотеза. Миша уже тогда интересовался шахматами, научил меня в них играть. Я помню, что 12 апреля 1961 года он мне поставил мат, а потом, по просьбе родителей, я поднялся к себе в квартиру и услышал по радио о полете Гагарина». Потом Алексей и Михаил учились вместе во «Второй школе», а шахматная карьера Цфасмана закончилась на уровне 1 разряда с одним кандидатским баллом. 

В свою очередь, Юлий Сергеевич Ильяшенко отметил, что «в стенах этого здания НМУ и МЦНМО существуют некий дух места. Мишина энергия и дух вносят очень большую составляющую в этот дух места». Виктор Матвеевич Бухштабер напомнил о том, что Цфасман и его коллеги основали Moscow Mathematical Journal, ставшим одним из ведущих в своей области. «Эта идея казалась абсолютно невероятной, но тот темп, с которым журнал был создан, и тот международный авторитет, который этот журнал получил, это замечательная заслуга Миши. Журнал позволяет молодым талантам быстро публиковать свои результаты и это не просто публикации, а признание более старших коллег». 

Юлий Ильяшенко (слева), Сергей Нечаев (в центре), Михаил Цфасман

М.А. Цфасман по-прежнему работает и в России, и во Франции. Он продолжает свои математические исследования на стыке алгебраической геометрии и теории чисел, пишет еще одну книгу. 

«Полит.ру» присоединяется ко всем поздравлениям в адрес рыцаря Ордена Академических пальмовых ветвей и желает ему дальнейших успехов!

 

Эндрю Уайлс. Фото: Alain Goriely/University of Oxford

Математик Эндрю Уайлс, доказавший в 1994 году Великую теорему Ферма, стал лауреатомАбелевской премии 2016 года. Премия, названная в честь выдающегося норвежского математика Нильса Хенрика Абеля, присуждается ежегодно с 2003 года и считается одной из самых престижных наград в области математики. Денежный размер премии составляет шесть миллионов норвежских крон.

Великая теорема Ферма утверждает, что не существует решений уравнения aⁿ + bⁿ = cⁿдля натуральных чисел больше двух. В 1637 году Пьер Ферма сформулировал это утверждения в заметке на полях трактата Диофанта «Арифметика», добавив: «Я нашел этому поистине чудесное доказательство, но поля книги слишком узки для него». С тех пор в течение столетий многие математики и еще большее число любителей пытались доказать данную теорему. Хотя так называемые ферматисты создали множество ошибочных доказательств, попытки доказать теорему принесли науке и немалую пользу. Давид Гильберт на II Международном конгрессе математиков сказал: «Проблема доказательства этой неразрешимости являет разительный пример того, какое побуждающее влияние на науку может оказать специальная и на первый взгляд малозначительная проблема. Ибо, побужденный задачей Ферма, Куммер пришёл к введению идеальных чисел и к открытию теоремы об однозначном разложении чисел в круговых полях на идеальные простые множители».

Эндрю Уайлсу сейчас 62 года. Он занимает должность профессора математики Принстонского университета и входит в научный совет Института математики Клэя. В 2000 году ученый стал рыцарем-командором Ордена Британской империи, а в 2005 году получил премию Шао.